VITS(Variational Inference with adversarial learning for end-to-end Text-to-Speech)是一种结合变分推理(variational inference)、标准化流(normalizing flows)和对抗训练的高表现力语音合成模型。
其运用了三种生成模型(GAN,VAE,FLOW),所以作为前置知识,我们先来学习三种生成模型
什么是生成模型呢?
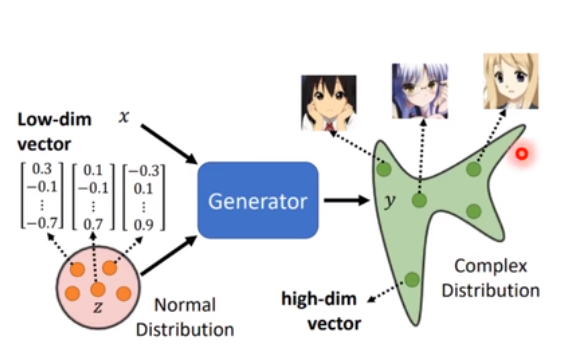
图像,文本,语音等数据,都可以看成是通过一个复杂分布采样得到的
怎么理解这句话呢,打个比方,你以极快的速度拍下两张照片,这两张照片看似是一样的,但经过处理后可以发现一些噪声、像素点是不同的,这是因为图片上的每个像素点可以看成是从一个高斯分布中采样得到的,而这个高斯分布的方差比较小,所以采样到的点有很大概率是相差不大的,所以两张照片看上去是一样的。这就是采样的概念。
每一个分布都可以由复杂的概率密度函数构造出来,一个简单的分布经过一系列复杂变换(如叠加)变成复杂分布的这个拟合的过程,就是生成器。而,一个简单分布中随机取一个数,将该数通过生成器生成一个复杂样本,这个过程就叫做生成。
1、GAN(Generative Adversarial Nets)生成对抗网络
GAN生成模型的作用是使生成的采样数据和真实数据尽可能的相似,其流程如下
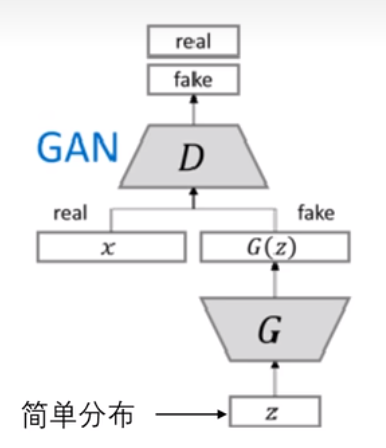
其采用竞争训练的方式,生成器G和鉴别器D交替更新
更新D时,固定G, 使得鉴别器D能够鉴别出真实数据x和生成数据G(z)
更新G时,固定D,使得生成器G生成的虚假数据能骗过鉴别器D
当训练完成后,可以舍去上面的部分,只保留这一部分
鉴别器D的Loss函数为
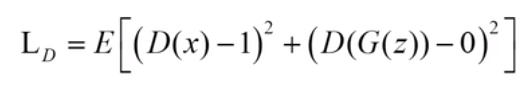
即当输入的数据为真实数据时,使得结果尽可能靠近1,当输入的数据为生成数据时,使得结果尽可能靠近0
生成器G的Loss函数为
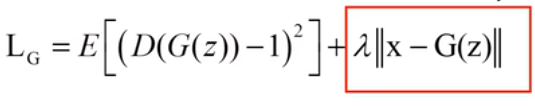
即使生成的数据被D识别的结果尽可能靠近1,有时候还会加入重构损失(即红色方框),这是要求不仅能骗过鉴别器D,还要求生成的数据与真实数据尽可能相似
2、VAE(Variational Auto-Encoder)变分自编码器
从AE(Auto-Encoder,自编码器)到VAE
在讲变分自编码器之前,我们先来讲讲自编码器
开头也讲过,生活中的很多数据(如文本,语音)都存在着大量冗余数据,理论上来说,他们都可以用极少的变量来表示,这种思想就是VAE的一个核心思想。神经网络最常见的一个作用就是分类,比如对于ai语音来说,输入层就是语音数据包含的所有数据向量,隐藏层捕获该数据的特征,输出层的个数一般就取决于分类的个数
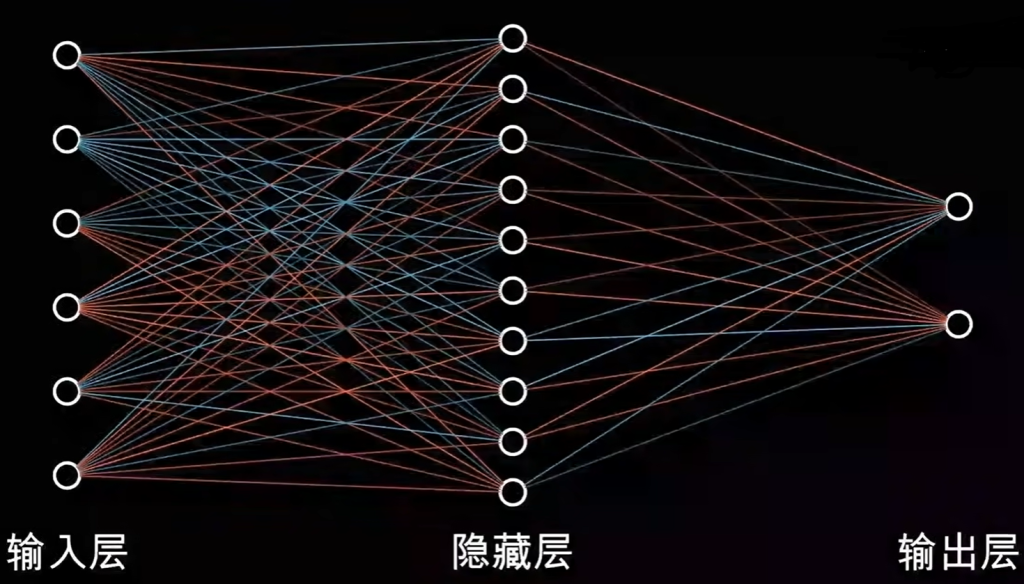
而AE(Auto Encoder)自编码器的“自”并不是自动的意思,而是自学习的意思,而AE与一般神经网络不同之处在于,AE包含了encoder和decoder两个部分,AE的输出为与原数据类似的东西,比如喂一幅画输出的就是一幅画,喂一段语音输出的也是一段语音,所以输出层的神经元数量和输入层是一样的,关键就在于隐藏层。
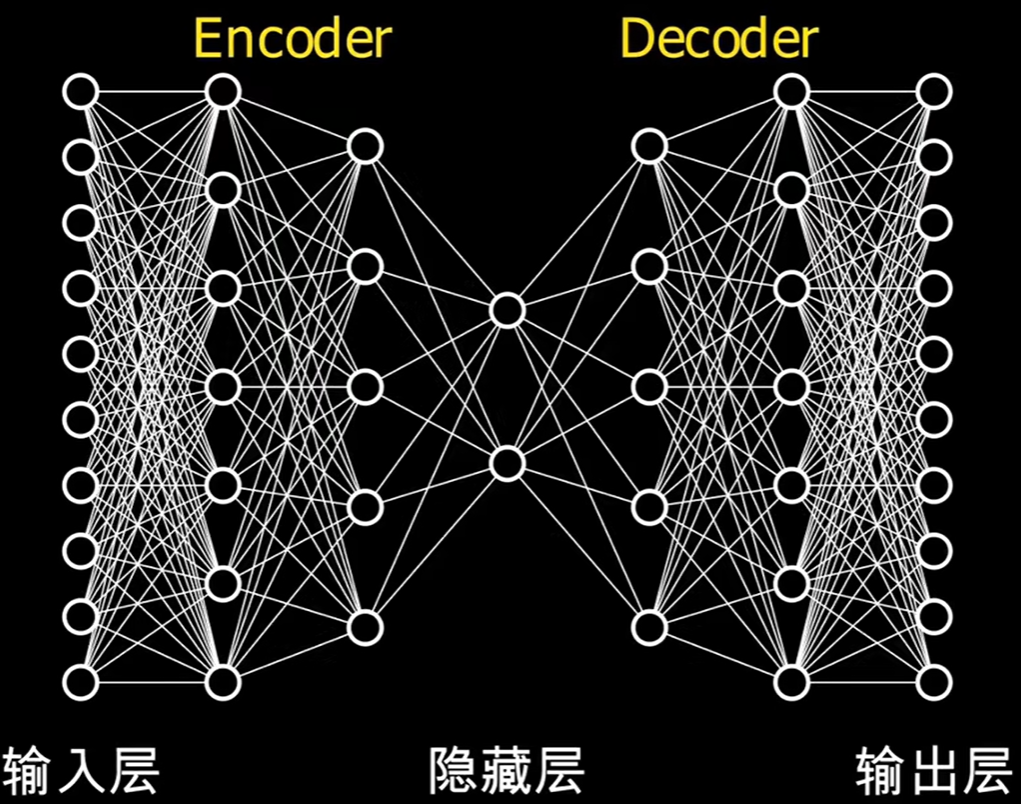
隐藏层的神经元数量非常少,其信息可视为高度压缩后的特征,即用很少的变量表示原数据。当然数量也不是越少越好,隐藏层的神经元数量越多还原的数据就越真实,AE的自训练就是通过重构生成数据与原始数据的损失函数来进行的。
而VAE与AE的区别就在于,在隐藏层这部分,VAE不再将特征映射到变量上,而是映射到某个分布上了,比如高斯分布,所以中间的部分变为如下所示
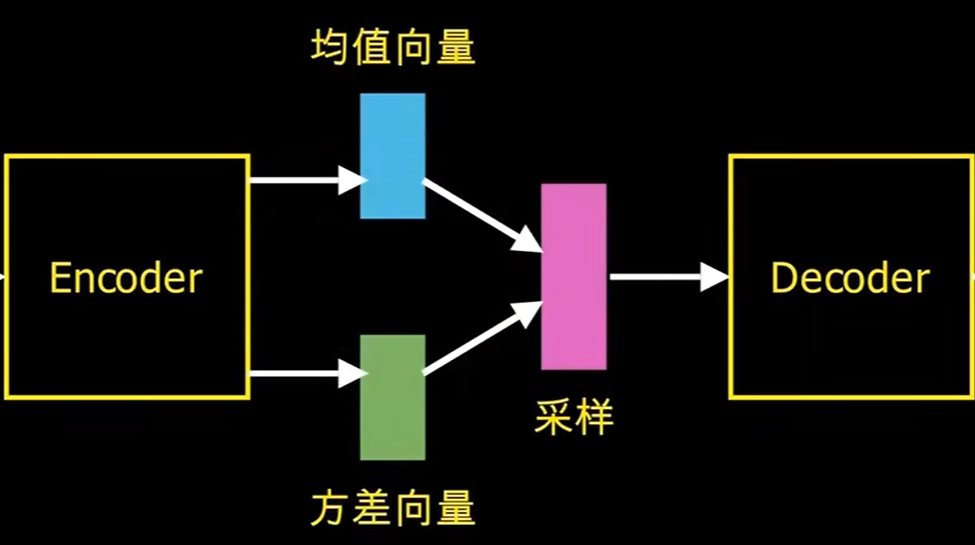
所以VAE的损失函数为
![]()
左边是重构损失,和AE是一样的,右边是KL散度,表示学习分布和高斯分布之间的相似性。那么,在了解了VAE训练的大体框架后,我们来看看VAE更详细的步骤。
VAE与GAN的比较
在介绍VAE的细节前,先和GAN做个比较。两者在目的上都是相似的,都是想构建一个从z到x的模型
具体的讲,是假设z服从某个简单分布(如正态分布),然后希望得到一个模型x = g(z),这个模型可以将原来z的分布映射到x这个分布上。也就是说,他们的目的都是分布之间的转换
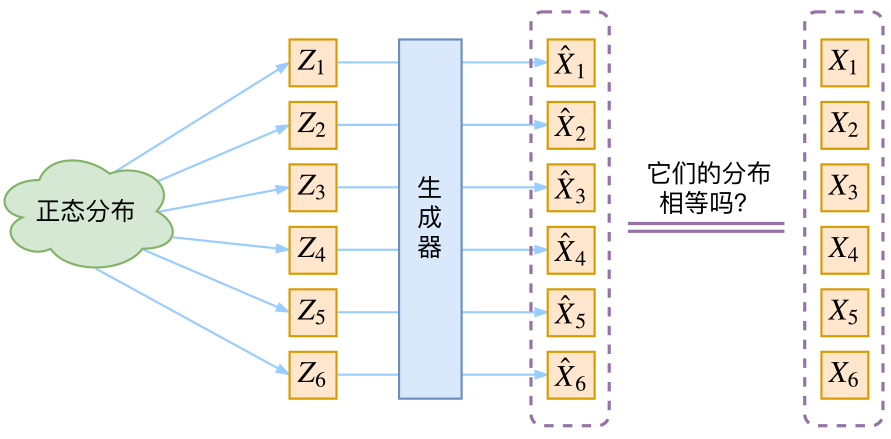
我们假设z就服从正态分布,于是我们取出若干个采样点z1,z2,z3......,然后对其做变化得x1 = g(z1),x2 = g(z2),x3 = g(z3)......,此时的问题是判断通过g生成的数据集的分布是否和我们想要的分布(即训练集的分布)相似。
这就是生成模型的一个难点,因为我们知道判断两个分布是否相似的办法是计算KL散度,但两个分布的表达式我们并不清楚,我们知道的只有两个分布中的若干采样点的信息,因此无法计算KL散度。此时GAN和VAE的处理方法就存在不同了。
GAN的处理方法比较暴力,既然不知道分布的表达式,那干脆不考虑了,我直接把鉴别真假的这个度量也用神经网络训练出来,也就是GAN模型的D。也就是说,GAN的鉴别器D鉴别的是采样点的相似程度。而VAE鉴别的是分布之间的相似程度,采用了一个稍微绕一点的方法。
VAE的推导及细节
损失函数的推导
重新梳理一下,我们的目标是得到复杂分布p(x),但p(x)的表达式建模很困难,所以引入了一个先验分布p(z),x先从简单分布中采样z,然后利用z生成x。根据贝叶斯公式:
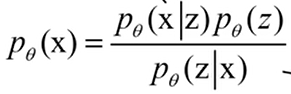
我们来一个一个看一下,分子的左部分表示在z的条件下取x,即生成网络G;分子的右部分表示简单先验;分母部分就比较复杂了,难以求解。所以对于p( z|x ),我们设计一个q( z|x )使得尽可能逼近p( z|x ),这个p( z|x ),就是VAE里的encoder编码网络,巧了,这正好是两个分布,所以直接计算KL散度来判断他们是否相似。
数学推导如下,具体计算就不详细说了,这并不是论文的重点。

在最后,这个式子正是我们之前提到的VAE的损失函数。
VAE流程中的细节
现在我们重新来看VAE的整体流程。
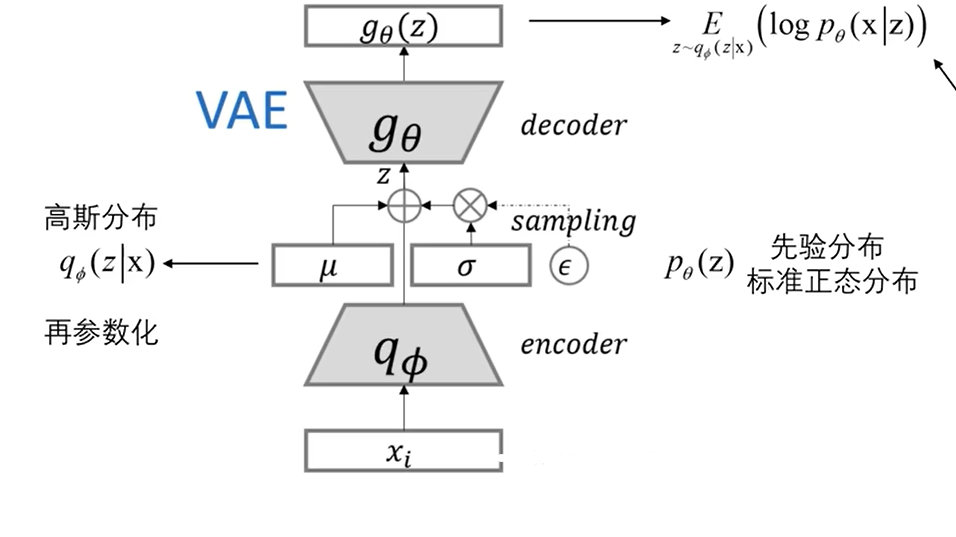
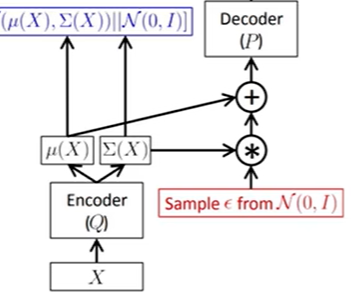
输入数据x经过编码后得到了一个均值为μ,方差为σ的高斯分布,现在需要对这个高斯分布进行采样得到z,然后送入decoder,也就是sample z from N(μ(x),σ(x))但问题是这个高斯分布是随机的,所以无法通过decoder后的梯度反向传播传下来,那么针对这个问题VAE就提出一个重参数化的技巧。重参数化的意思是任何一个高斯分布都可以看成是均值+标准差×标准高斯分布的形式,也就是说任意一个高斯分布都是关于标准高斯分布的一个函数,即:
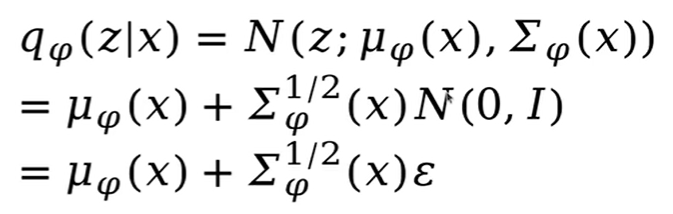
有了重参数化,我们将采样过程调整为右图所示,此时的采样为sample z from N(0,1),然后再与u和σ进行相加相乘得到我们想要的高斯分布,最后送入decoder。至此,整个流程中没有任何随机的部分。
VAE总结与条件VAE
那么VAE的核心部分就基本上介绍完了,再重复一遍,GAN是采样点的接近,VAE是分布的接近。这里介绍的是一般的VAE,实际上vits里用的是条件VAE,条件VAE就是把p(z)改成了p(z|c),c指要求满足的条件,也就是说z的采样不是从标准高斯分布N(0,1)中取,而是从N(μ,σ)中取,这里的均值和方差是固定的,其值取决于输入的文本(文本转语音的文本),因此也不存在随机的部分。
3、Flow(Normalizing Flow)流模型
flow模型作为生成模型一开始并没有像GAN和VAE那样热门,这不仅仅是因为flow没有像GAN那样直观的解释,还和flow通篇的数学证明有关,而且当时flow的效果也不尽如人意,所以学习flow的人不多。但在ai绘画兴起后,其运用的基于flow模型的glow模型起到了很好的效果,因此flow模型才渐渐进入大众的视野,并在之后的ai语音中也运用到了flow模型。
说实话我是非常不擅长从一堆数学推导中理解一个生成模型的,所以flow模型的学习对我来说是最痛苦的,因此关于flow模型的介绍我只能说尽量用我能搞懂的语言解释一下。
flow的推导
前面我们提到,GAN模型采用的是采样点的逼近,VAE模型采用的是分布的逼近,两者都是逼近,而flow的思想是直接找到映射关系,也就是说用一个式子直接把两个分布之间的映射函数找出来。那么两个分布之间可以用式子表达吗?我们看一个简单的例子
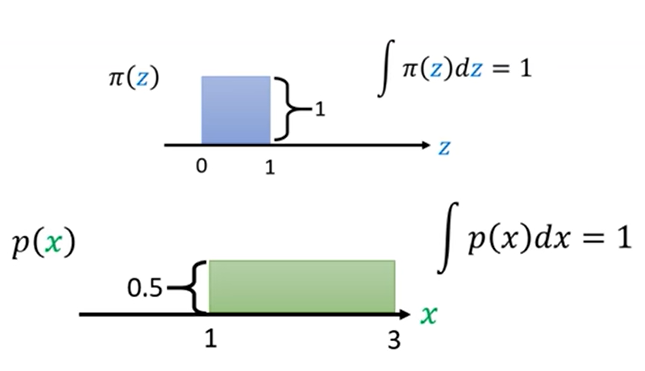
、
其中π(z)为简单的均匀分布,p(x)为复杂的均匀分布。显然,两个分布之间的关系很容易看出来为:
x = f(z)= 2z + 1
延伸到复杂分布(不均匀的分布)
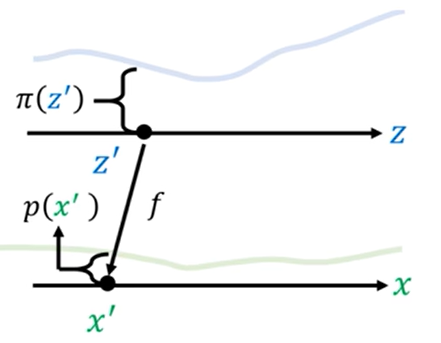
此时我们想找出z‘→x’之间的关系,这里引入微元的思想,将极小的一段Δz内的分布看成是均匀分布,同理Δx内的极小一段也看成均匀分布。如下图
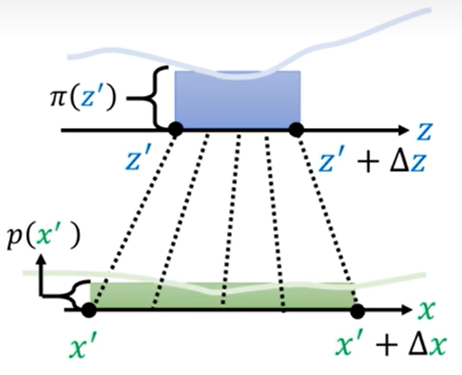
此时满足蓝色的面积 = 绿色的面积
即:π(z’)Δz = p(x’)Δx
移向得:p(x’)= π(z’)Δz / Δx
将其看成微分形式为:p(x’)= π(z’)dz / dx
而dz/dx可能为负值,所以再加上绝对值符号,所以复杂分布之间的映射关系我们也找到了,为:
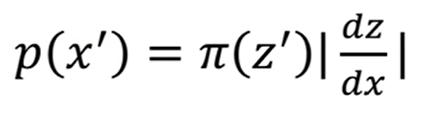
继续衍生至多维的复杂分布
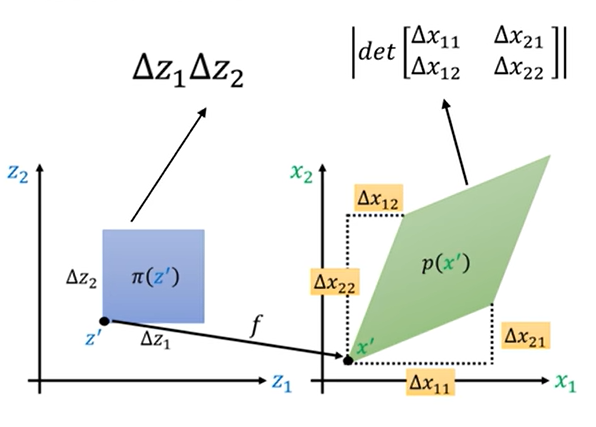
对于π(z’),分别在水平和垂直方向上移动了极小的距离Δz1与Δz2,那么映射到p(x’)上就不一定是垂直和水平的移动了,对于一般情况即斜着移动的情况,p(x’)与之对应的映射应该是个平行四边形,此时蓝色的面积为Δz1Δz2,绿色的面积为行列式的绝对值。
同样的,概率×面积相等,移向,视为偏导形式,最后det里面正好是雅各比矩阵
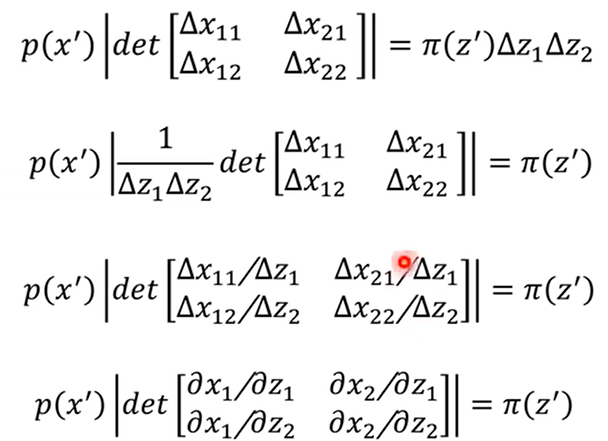
至此,多维复杂分布之间的映射关系就得到了,即p(x’)乘上雅各比行列式的绝对值等于π(z’),其正向变化与反向变化之间的式子分别是:
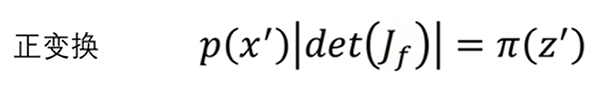
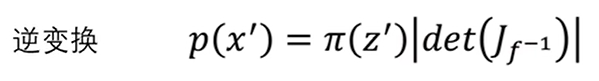
也就是说如果x与z之间的函数关系知道的话,各个变量之间相互求导得到雅各比矩阵,然后就能得到分部之间的映射关系了。到这一步,flow模型的基本思路就出来了
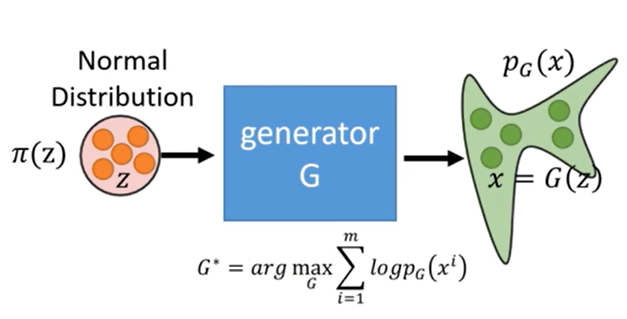
其中z到x的映射关系就是图中的生成器G,也就是求雅各比行列式的绝对值,看起来一句话就说完了,但有两个困难,一个是这个G怎么求,一个是知道G求雅各比的计算量也非常大,所以接下来来看flow的训练过程
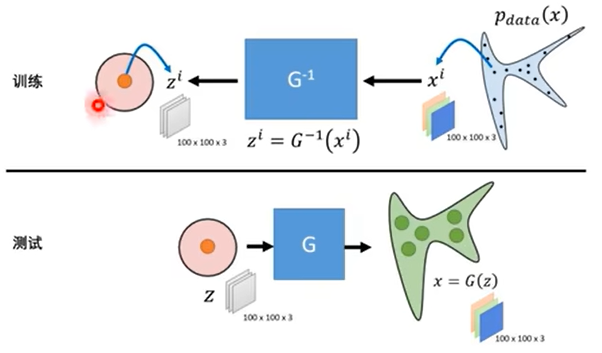
对于训练过程,首先我们有一堆复杂数据(训练数据)Pdata(x),视为是复杂分布中采样出来的,然后通过G的逆生成数据z’,然后从简单分布中也采样出若干数据z,使得z与z’尽可能相似,测试过程相反,将z通过G生成x,看是否符合G(z)。显然,flow的一个显著特点就是可以双向转换。
生成器G的内部
那么现在,我们来看看G的内部是什么样的
为了使G的逆可以计算以及计算雅各比矩阵时轻松一些,flow引入了一种称为耦合层的设计
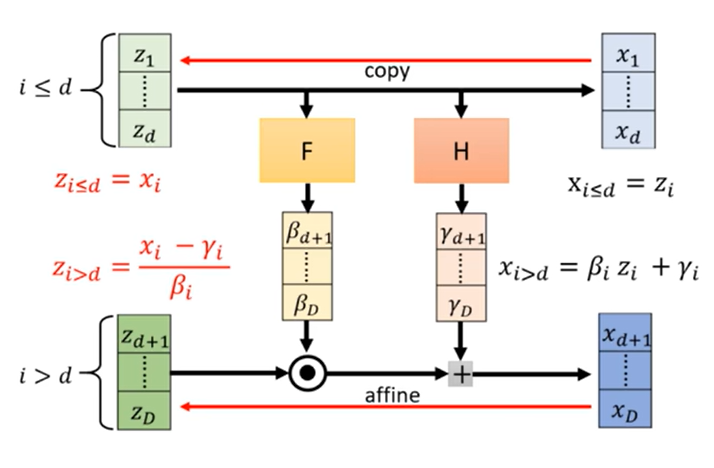
我们知道,flow求的是z到x的映射函数,也就是说点与点之间一一对应,所以z和x的维度是一样的,假设都为D。此时将其分为1~d及d~D两部分,即z1~zd对应x1~xd,zd~zD对应xd~xD。前一部分不变(copy),后一部分令x等于z乘一个数加一个数(affine),这两个数是F和H这两个神经网络训练得到的。那么反过来,由x→z我们将式子移向也能得到对应的关系,对应关系如下:
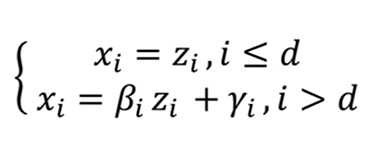
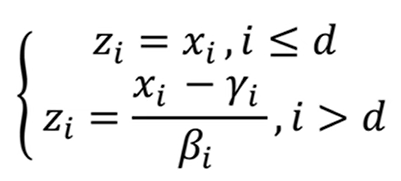
有了耦合层这个设计后,雅各比矩阵就好算了,也就是计算x元素分别对z元素的求导
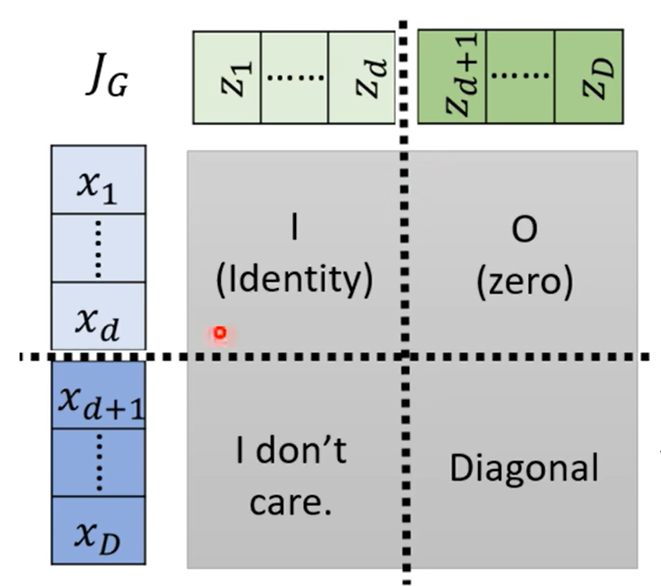
来看这个矩阵,以d为分界线将矩阵划分为四个部分,其中左上角表示x1~xd与z1~zd的对应关系,即x=z,所以这一块是单位矩阵。右上角表示x1~xd到zd~zD的对应关系,二者无对应关系,所以结果为0。右下角表示xd~xD与zd~zD的对应关系,求导后剩下系数βi(d<i<D),根据分块矩阵的性质,行列式等于主对角线相乘,所以不用管左下角的结果是什么,其值就等于左上角×右下角,即:
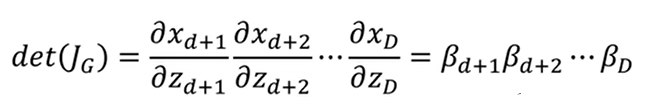
反过来也很简单,结果为这个值的倒数,推导过程是一样的
通过这个式子我们可以容易的实现建模,但这个式子比较简单,因为xi只与zi有关系,和其他的z没有关系,所以这个的建模能力是比较弱的,那么为了实现比较复杂的建模,我们将多个耦合层链接到一块,实现多模块耦合,并且在单耦合层时我们令前一部分copy,后一部分affine,在多模块耦合时,我们交替着进行,这样能让建模的效果更好。
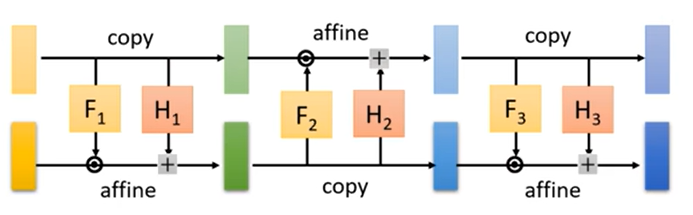
G的内部就是这种构造了,flow的训练会经历多个G的迭代,这样最后拟合的效果就会越好越好

至此,flow的基本流程介绍完毕。
4、VITS模型
介绍完三种模型后,我们来介绍vits模型对这三种模型的运用
从整体框架来看,vits是一个大的VAE模型,建模的部分用到了flow模型,训练的部分用到了GAN模型,整体结构如下
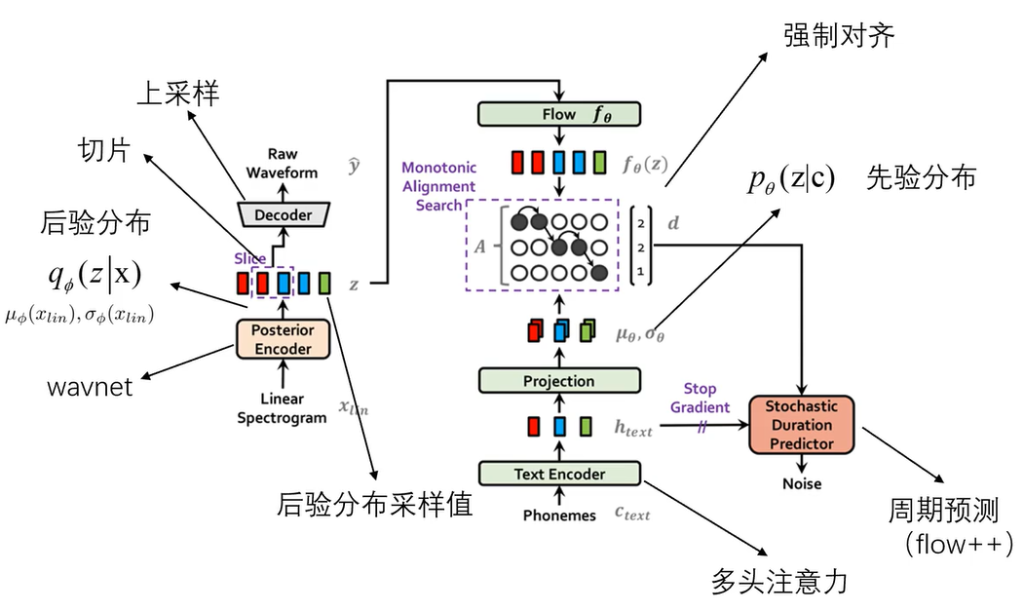
先看左边,我们要的是文本转语音,所以训练数据肯定要是语音数据,所以最下面的Linear Spectrogram就是音频文件的短时傅里叶变化后的频谱,然后经过encoder后得到后验分布q的μ和σ,由μ和σ决定的分布中取出z,z经过decoder后输出的也是一个音频,这就是端到端的意思,像以前的语音训练模型,输入和输出的都是语音文件的特征,所以之后还要再训练一个神经网络,vits模型就省去了这些麻烦
前面也讲过,VAE损失函数说明VAE要考虑输入输出相似和后验分布和前验分布相似,这里的前验分布就是p(z|c),由于vits输入的是文本所以这个条件c肯定是由文本决定的,phonemes这个部分就是将输入的文本展成音素,中文的话就是拼音的声母和韵母这些,然后结果text encoder变成一系列特征,这些特征再经过一个projection映射层变成p(z|c)的参数。下一步应是计算前验分布和后验分布的KL散度,但这里可以看出来二者维度不同,是不太好计算的。文本的特征显然是比语音数据的特征少的,所以直接用公式计算KL散度是不现实的,只能回到KL散度的定义(原始公式)上,公式为:
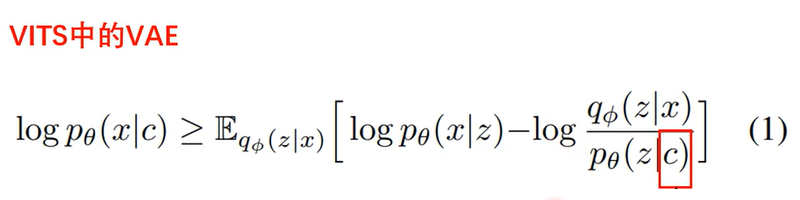
这个公式在介绍VAE的时候也见过,无非就是把p(z)换成了p(z|c),前面的log是重构误差我们不管他,看的是后面的log部分,这部分的意思是z是从q中采样出来的,现在要把z带入q中求似然值,然后再把z带入p中求似然值,两者相减。
q(z|x)这部分再encoder后就得到了,q这部分再经过了一个flow模型变成了f(z),这里让q进行flow训练的目的是让q有更好的信号表达能力。那么现在的问题就变成了f(z)和p(z|c)之间,这里引入了一个强制对齐(DTW)的方法。
DTW是一种基于动态规划(DP)思想,用于解决语音长短不一致的模板匹配问题,是早期语音识别领域运用到的一种几乎不需要额外计算的方法,因此DTW只是一个简单的强制对齐的过程,而不是神经网络的训练那么复杂的东西。
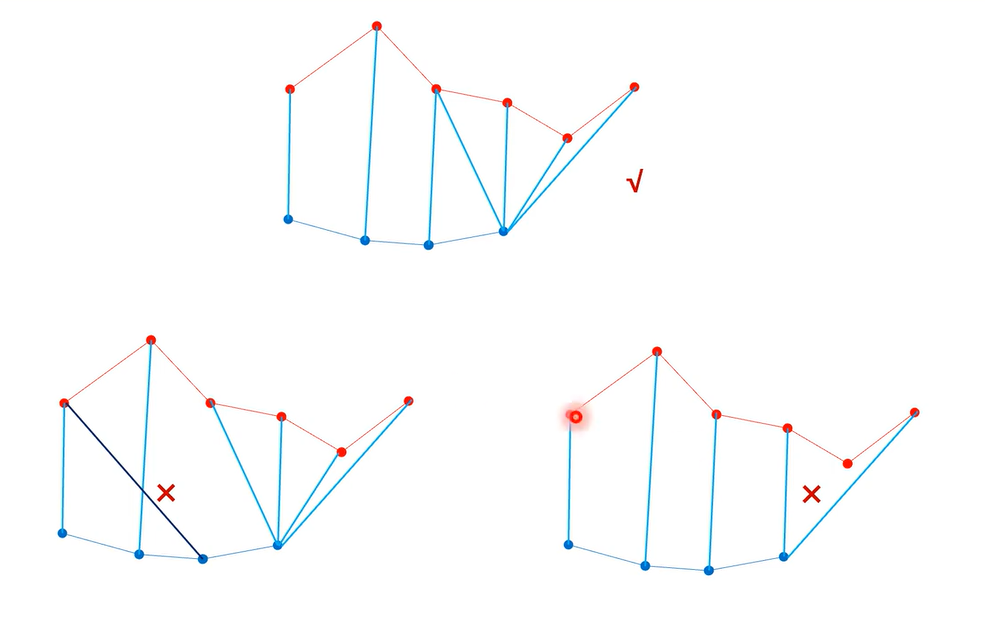
我们假设有需要对齐的两个序列,上面的序列比下面的长,DTW算法的规则是一一对应,不能回头,不能有空。图中的第二个犯了不能回头的错误,第三个犯了不能有空的错误。当然,即使有这三个条件,符合的匹配方法也有很多种,我们需要的是连线之后匹配长度最短的那种情况
继续,将DTW运用到vits的强制对齐当中,上面的序列为f(z)的一系列采样点,下面的序列为一系列分布,按照上面的介绍,平均距离最短的是最好的匹配,在这里,匹配指把上面序列的某一个采样点带入下面序列的某一个分布中算似然值,似然值总和最大的匹配情况就是最好的匹配结果。具体的算法实现就是该点的距离+左下角两个中较大的那个数(这里只有左下两个,因为采样点可以带入多个分布,而一个分布不能对应多个采样点,也就是文本可以对应多个音频,音频不能对应多个文本),这里就不展开介绍了,可以去看DTW的算法实现。
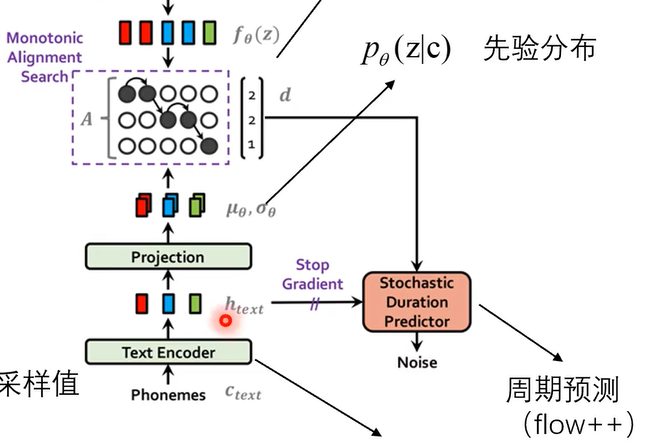
那么通过强制对齐配对好后,我们从图中可以看出这里分布与采样点对应的情况是2,2,1,于是我们就知道了时长。接着将A矩阵中的2,2,1这几个周期视为分布,进行周期预测,这里本质上用到的也是flow模型,也就是为了表示效果更好,把分布转换成了另一个分布
至此,vits的整体模型流程就介绍完了。接下来来分析一下vits的损失函数,分为几个部分
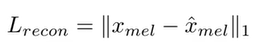
这一部分是VAE模型的输入输出相似程度。前面也说过,在vits这个模型中,输入是短时傅里叶变化后的频谱,输出是音频,二者是无法直接计算相似度的,所以将输入值经过梅尔滤波器(梅尔滤波器是一种常用于语音信号分析的数字滤波器.它的作用是将频谱分成固定数量的带宽,每个带宽代表一个梅尔频率,以模拟人耳的听觉特性)之后变成一个fbank,输出值也变成fbank,转移成对mel特征的相似度计算。
(fbank:人耳对声音频谱的响应是非线性的,Fbank就是一种前端处理算法,以类似于人耳的方式对音频进行处理,可以提高语音识别的性能。获得语音信号的fbank特征的一般步骤是:预加重、分帧、加窗、短时傅里叶变换(STFT)、mel滤波、去均值等)
![]()
这个是VAE模型的后验分布q与前验分布p的误差,前面介绍过,Ctext是由输入文本决定的条件,A是强制对齐后的矩阵。
对于VAE模型的损失函数就只有这两个了,但vits还结合了GAN模型。在输出Raw wavefrom后,输出的这个结果要经过GAN网络的鉴别器D,所以还有以下几个损失函数:
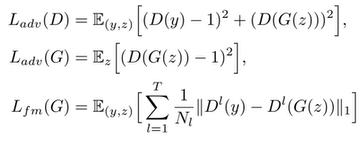
前两个就不多说了,标准的GAN模型损失函数,值得一提的是这里虽然只写了一个D(y),但实际vits模型中是有一组D的。对于最后一个函数,我们将原始数据和生成数据同时输入鉴别器D中后会经过很多神经网络层,这个损失函数的作用是让这些中间层的结果也尽可能相似。
此外,在周期预测这里还有一个损失函数Ldur,表示让强制对齐后的分布(把矩阵看成分布)经过转变后尽量接近标准正态分布。综上,vits的总损失函数为
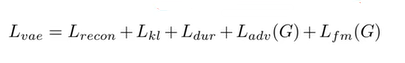
需要补充的是,神经网络的训练是靠损失函数来反映训练的好坏的,但语音数据有长有短,也就是说在其他条件不变时,长的语音数据更可能有高损失,这样就无法判断实际训练的好坏,所以vits的损失函数并不是在编码后将所有数据进行损失计算,而是在编码后先进行一小段切片(也就是图中的slice部分,时长大约30秒),然后只对这slice部分进行解码,这样就避免了损失函数无法反映真实训练情况的问题。
训练完成后,用训练出来的模型进行推理
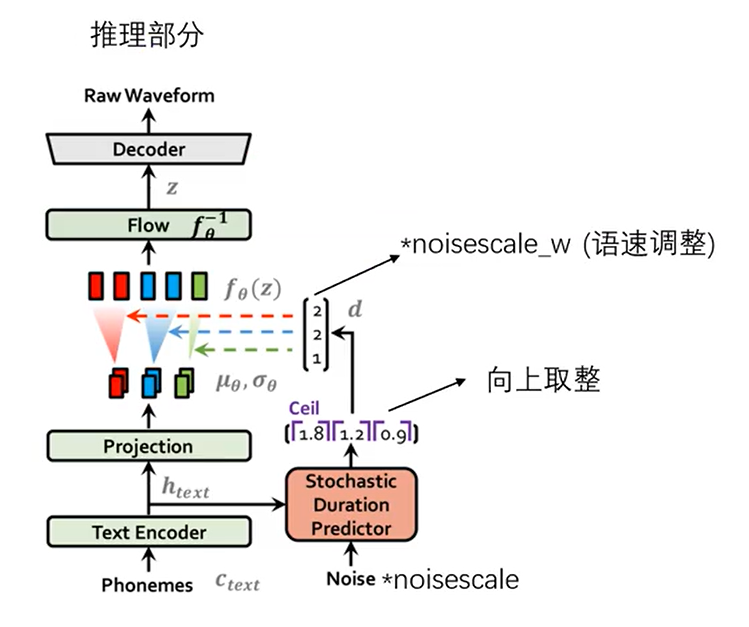
推理部分也非常好理解,整体就是一个VAE。需要额外说明的是Noise部分的输入是一个随机的正态分布,因为周期预测这块用的是flow,flow具有双向转化的功能,所以根据输入的noise可以反过来逆推合成语音的时长。
至于为什么要向上取整,解释这个之前要回到训练模型的图中。在训练模型的强制对齐中,因为是一一对应,所以矩阵里的值一定是整数,下一步是通过flow模型变成正态分布,也就是将整数变为随机数,这里用到的方法是用d-u,u是0到1之间的随机分布。所以在推理部分中,noise生成的不是d,而是d-u,所以要把u加回去,即向上取整。
向上取整后,比如图中是2,2,1,然后将分布按数值复制,再经过一个flow的逆向转换,也就是得到一系列q的采样,最后decoder,得到音频。



Comments NOTHING