深度学习基础介绍
机器学习就是找到一个人类写不出来的函数。例如语音识别的输入是一段波形,输出是一段文字;图像识别的输入是一张图片,输出是一段文字;阿尔法狗的输入是棋盘上的黑子白子位置,输出是下一步下在哪个位置。
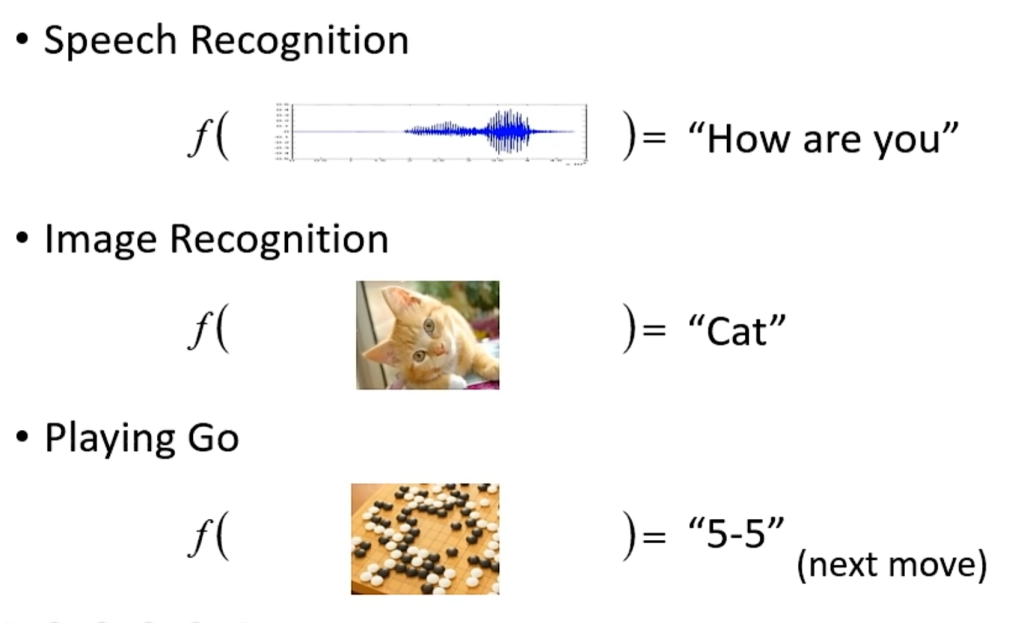
而深度学习是机器学习中的一个领域。机器学习的目的是找到一个人类写不出的函数,深度学习就是用类神经元来构造这个函数
深度学习的分类
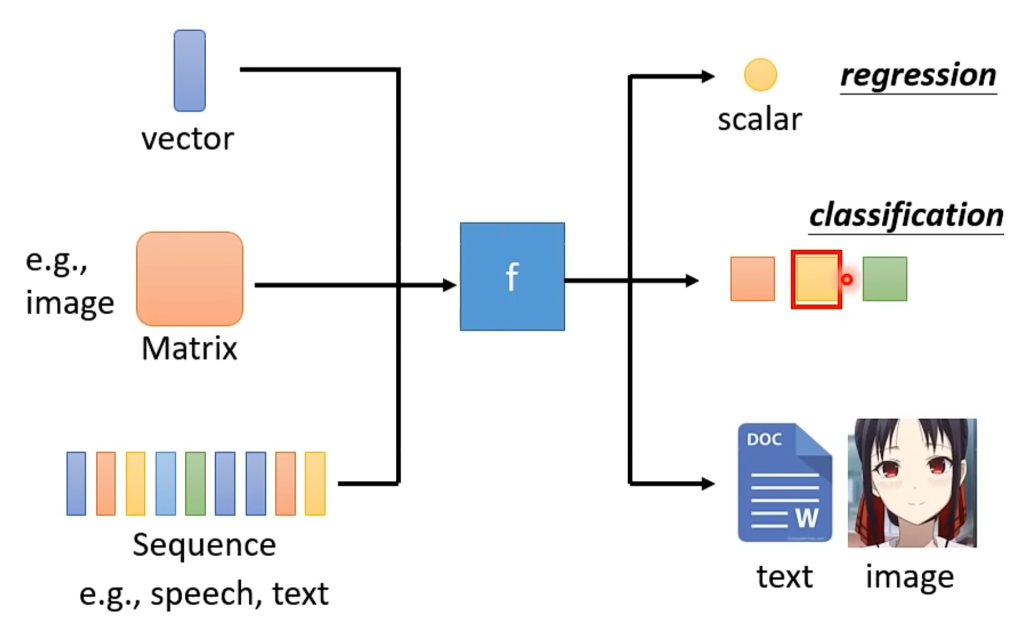
深度学习的输入可以分为很多类,比如向量(vector),矩阵(Matrix),序列(sequence),输出也可以分为很多类,比如数值(scalar),类别(classification),甚至直接输出一段文本或者图片。
输入图片时一般转换为矩阵,输入语音、文本时一般转换为序列;输出为数值时称为回归,输出类别时称为分类,输出文本图片时称为生成结构化数据。
机器学习的步骤
以预测某个博主的每天视频流量为例子:
第一步:根据猜测先写出一个函数
先猜测当日的流量是不是和和前一天的流量有关,于是猜测函数关系为y = b + wx,其中y是预测值,w是权重,b是偏差,x是前一天的流量。
第二步:构造自己的损失函数L(b,w)
假设b=500,w=1则按照已有的数据列出预测值和真实值之间的差距。

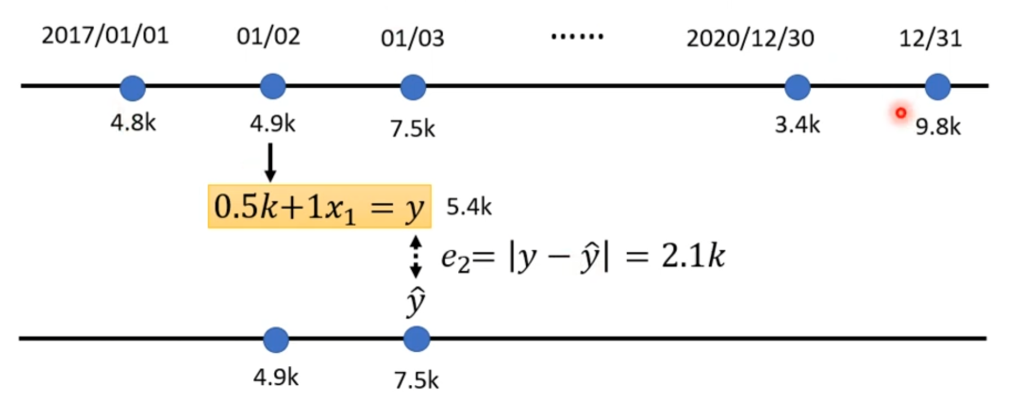
然后把数据集全部的偏差值取平均,就是Loss
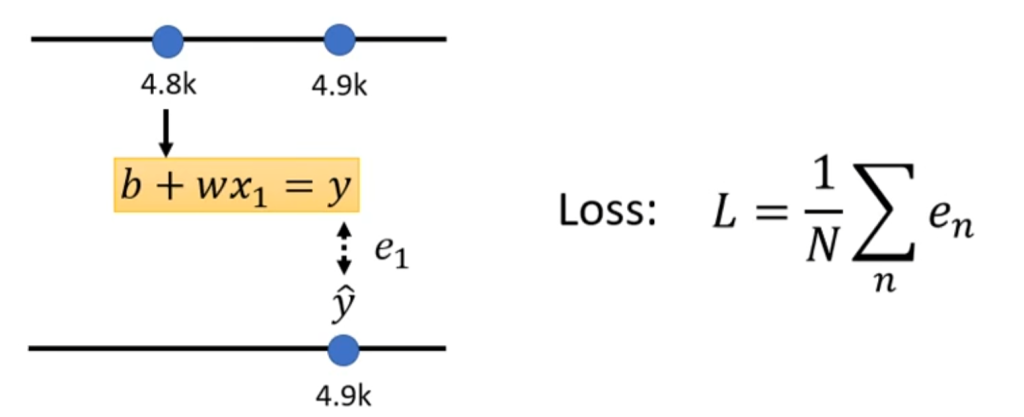
当然,损失函数也不一定必须用差值,用差值的平方也是可以的,这种还可以放大差值大于1的部分。所以损失函数的选择要具体情况具体分析。

那么,怎么判断一个Loss的好坏呢,上面举的例子是b=500,w=1的情况,实际上机器学习会把所有的b和w的取值列举出来并计算Loss,这种表现Loss的等高线图叫做error surface,如下图,越靠近灰色代表预测越精准。
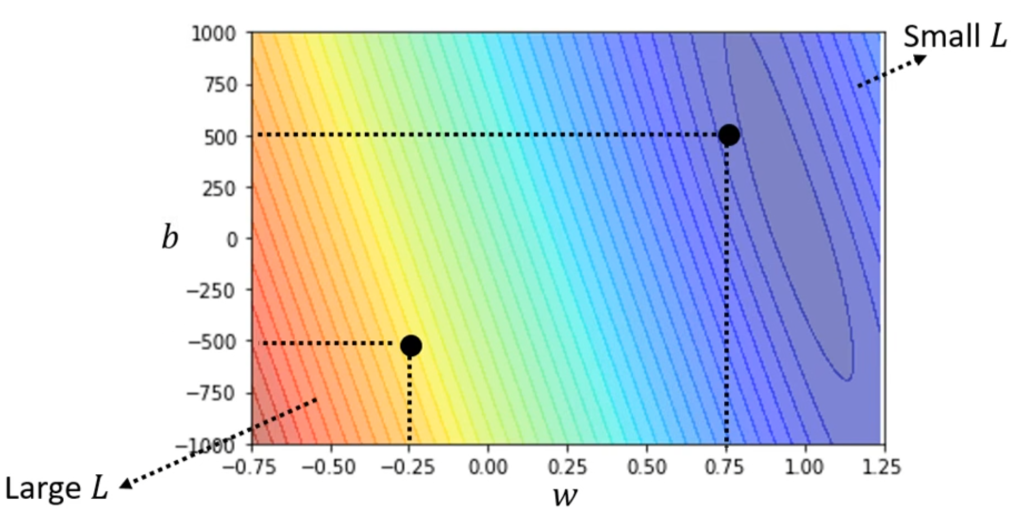
第三步:优化
优化的目的是找到最优的w和b,使得Loss最小,即:
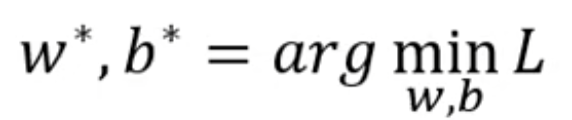
这就需要梯度下降(gradient descent),为了解释梯度下降,我们先从一个变量讲起。若只有一个变量w,则可以画出Loss曲线,例如下图:
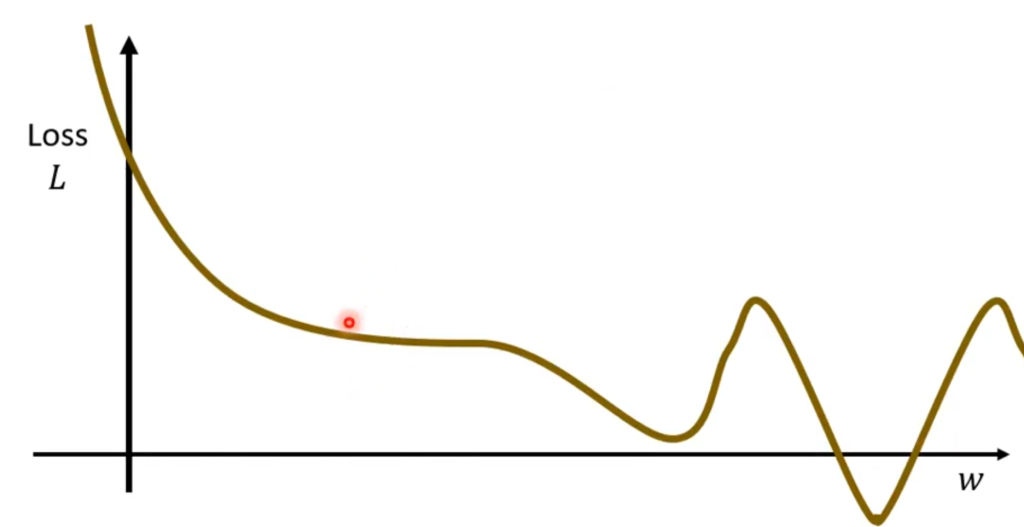
η梯度下降的步骤为:先随机定一个w0,再计算该点的微分,从图上理解为该点的斜率,如果斜率为正则向左移动,反之向右移动,可以形象的理解为向局部最低处走。
那么走的幅度多大呢,取决于两方面。一是微分的大小,也就是越陡走的幅度越大;二是学习率,用η表示。学习率是自己设置的,这种由自己设定的参数称为超参数 ,显然,Loss不是超参数。
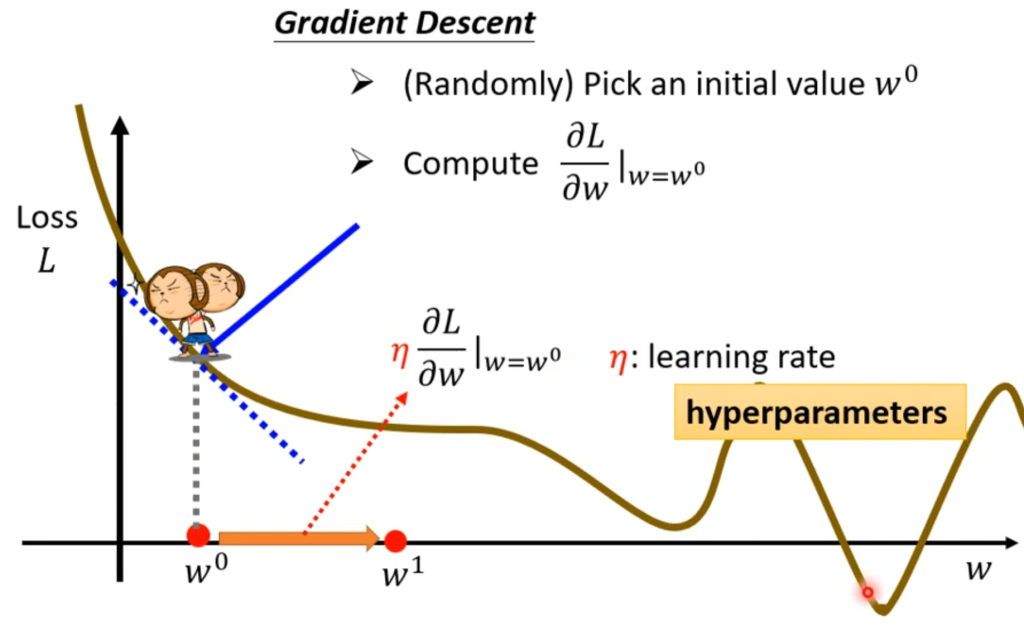
于是,第一次的优化过程为:
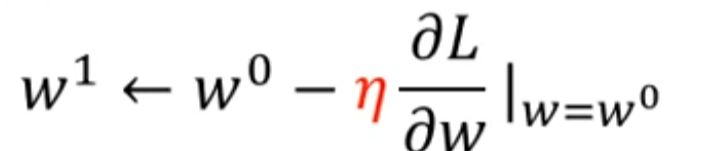
如此循环往复,什么时候停止呢?一种情况是你设定迭代步数,例如我提前设置迭代一万步就停止。另一种是迭代到了局部最优处,这种情况再继续迭代将不会更新w值。
此时明显有个问题,那就是局部最优解明显不是全局最优解。但是实际情况下局部最优解通常就是全局最优解,难点并不在这里,这个后面再说。
那么引申到两个变量也是一样的,先随机选一个w0和b0,然后分别对二者求偏导,开始迭代。最后在二维等高线Loss图中的表现为:
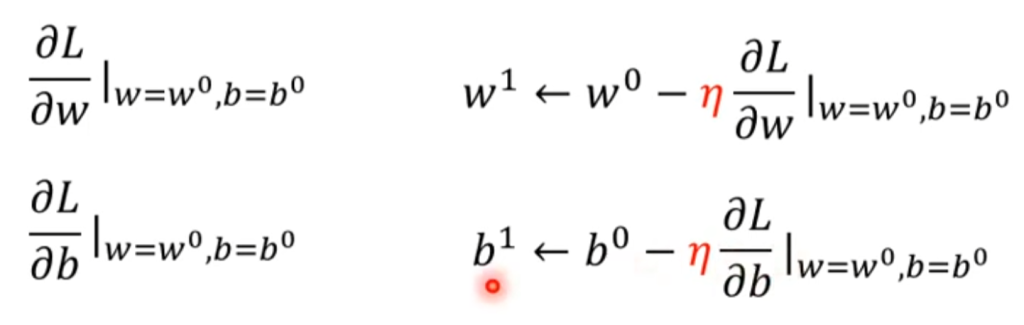
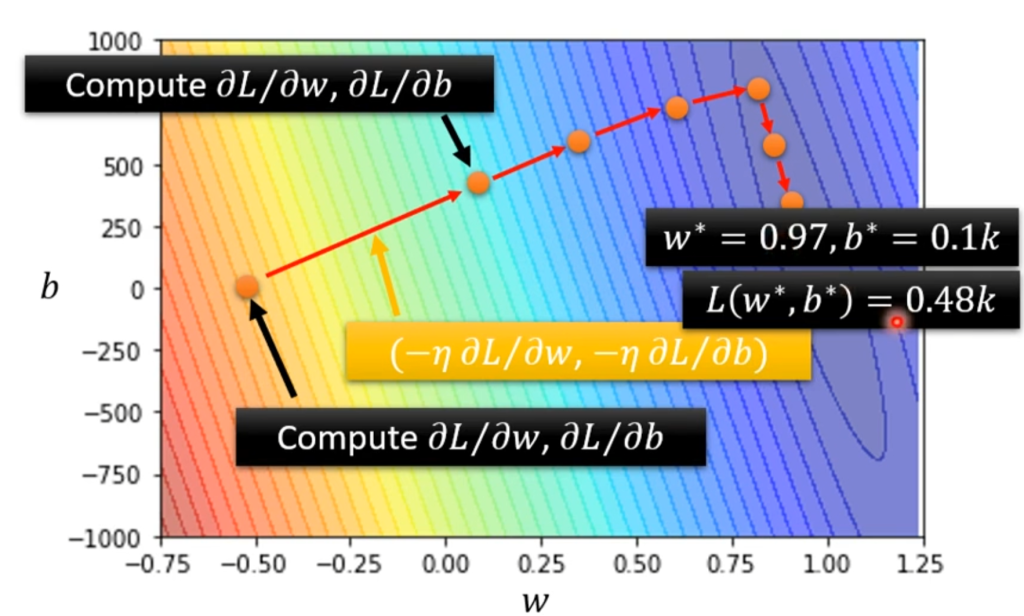
根据训练后的结果进行调参
以上三步称为机器学习中的训练(train),第一次训练后的预测值与实际值的情况如右图:
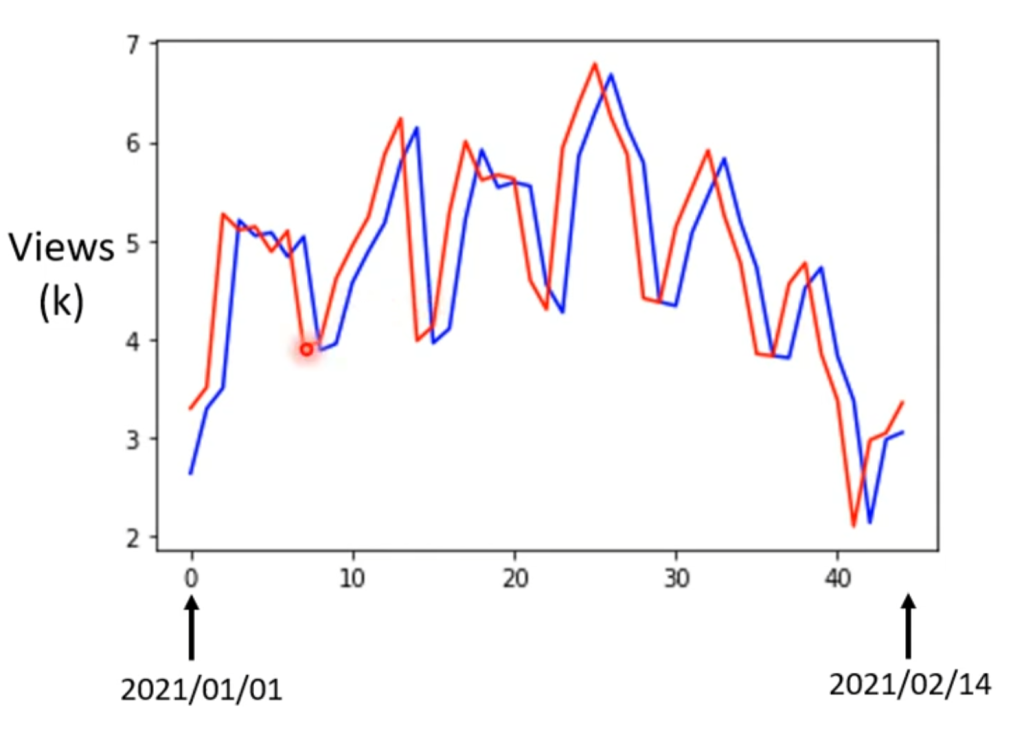
从图中可以看出流量具有周期性,因此可以推测不仅和前一天的流量有关,可能和前七天的流量有关,于是可以调整第一步的函数构造重新进行训练,再看效果。依次用前七天,前28天,前54天进行训练,得到的效果如下:
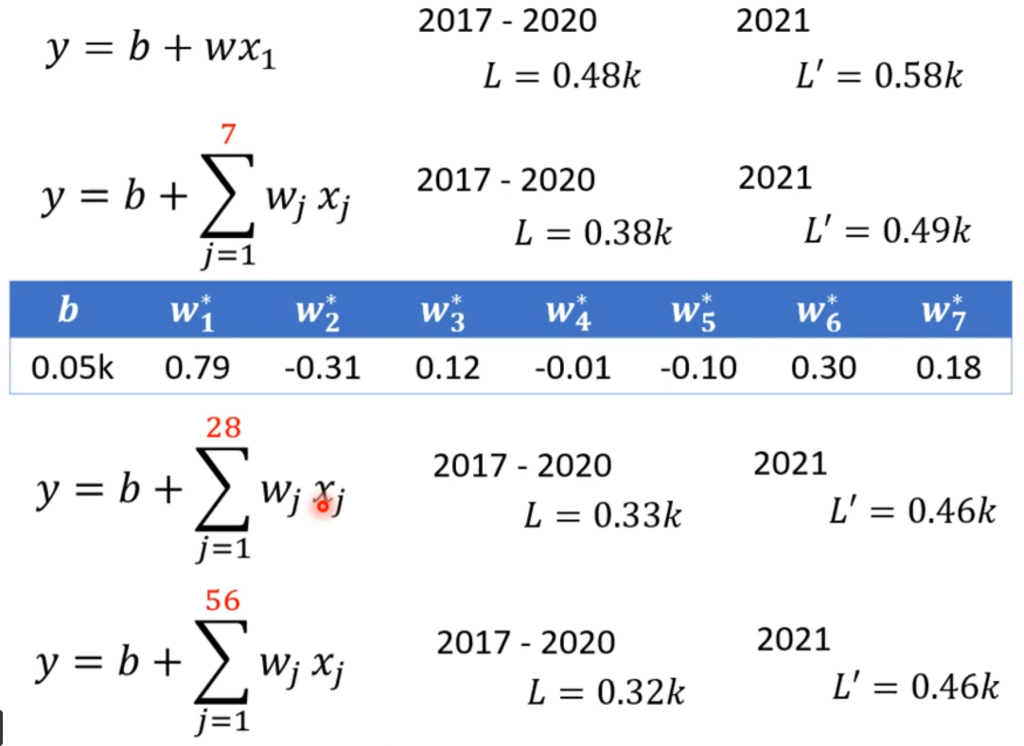
可以看出超过28天后,继续提升天数的预测效果并没有更好。
模型误差以及优化
上面的例子存在一个问题,那就是我们模型假定的是y = b +kx,这是一条直线,但现实的情况可能是折线,这就需要用更复杂的函数构造出折线。
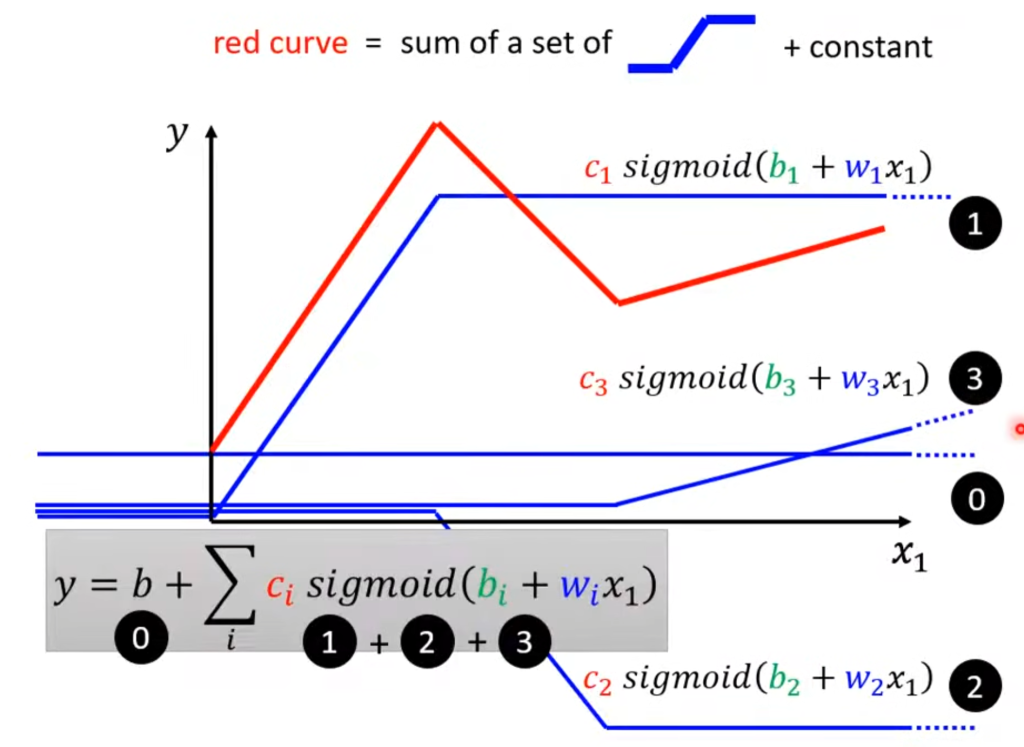
任何一条折线都可以分解成一个常数和若干个标准折线的叠加。例如下图,红色的折线可以视为所有蓝色线的叠加。
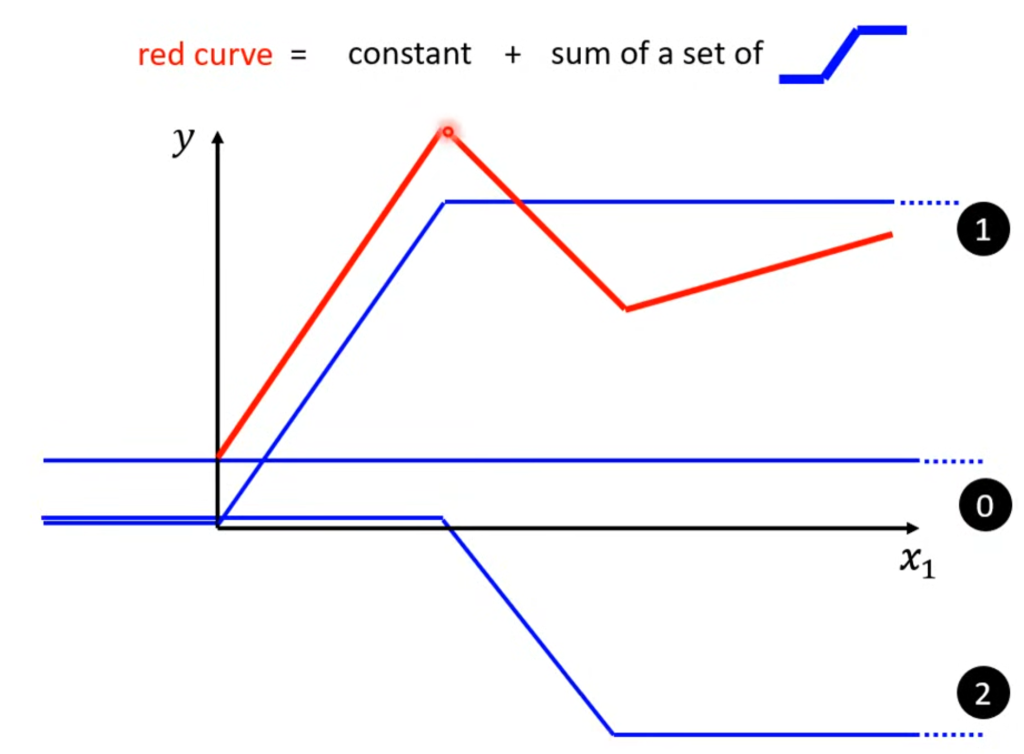
曲线可以近似的用折线表示,而折线又能用常数+若干标准折线表示,意味着只要有足够多的蓝线,就能表示任意一条曲线
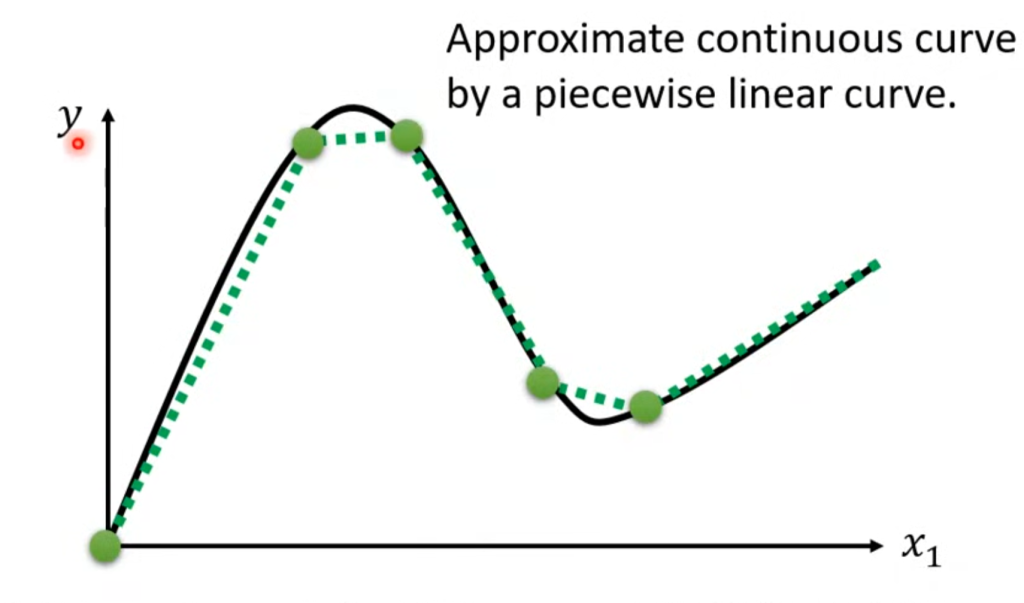
那么标准折线怎么用函数来表示呢?我们可以用曲线的函数来逼近折线
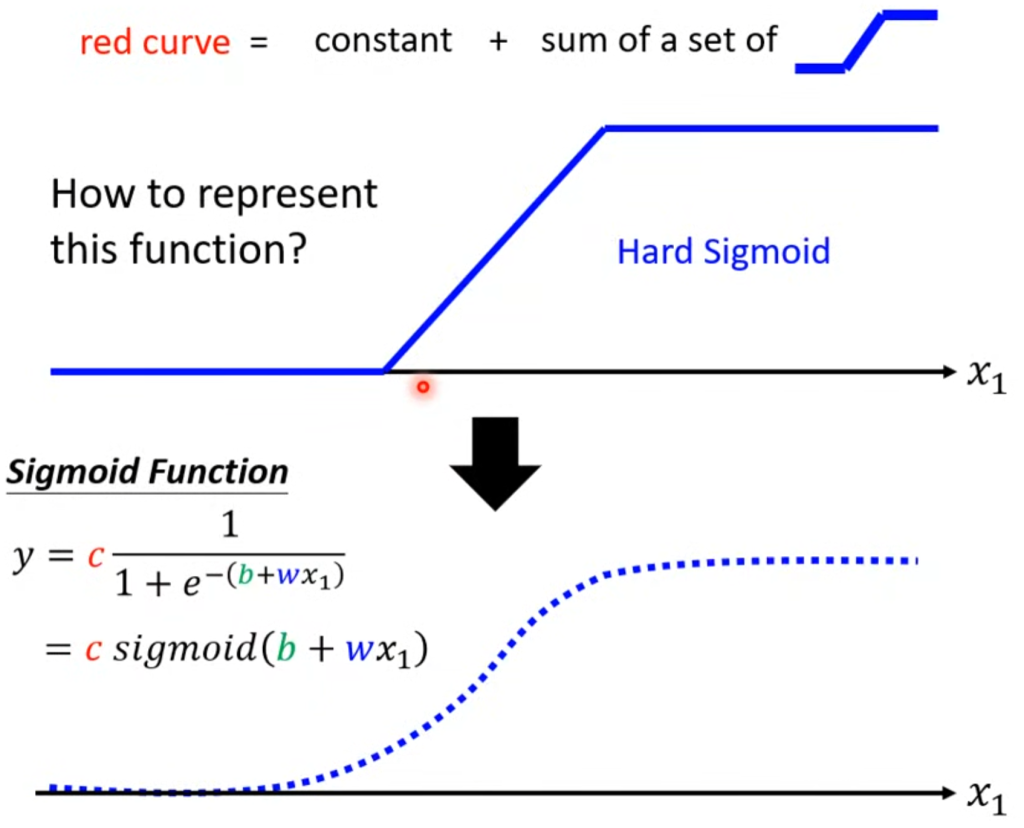
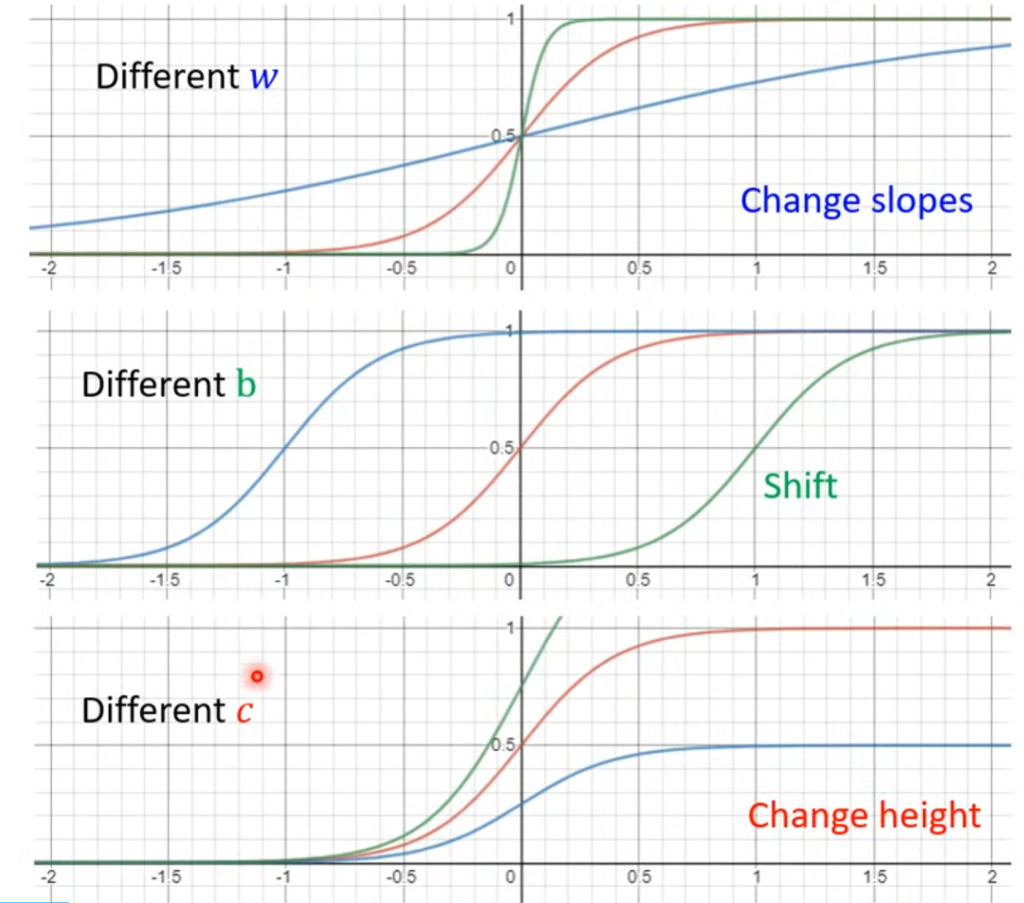
其中,改变w会改变斜率,改变b会左右移动,改变c能不改变形状改变高度
现在回到开始的那个红线,可以如下表示
到这里,我们可以对预测流量的构造函数这一步进行优化,并且引入前七天流量相关,让函数的表达能力更强

于是,我们将机器学习三步走的第一步由y=kx+b改为这种更复杂的形式。(图中用的线性代数的表达方式,和上面这个函数是一样的)
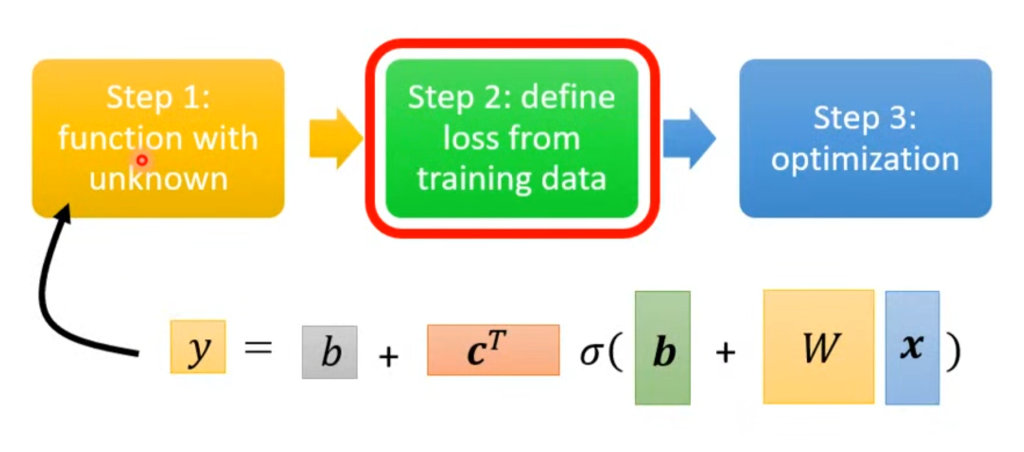
θ第二步也是一样的,带入参数计算出预测值和真实值之间的差距,作为Loss函数
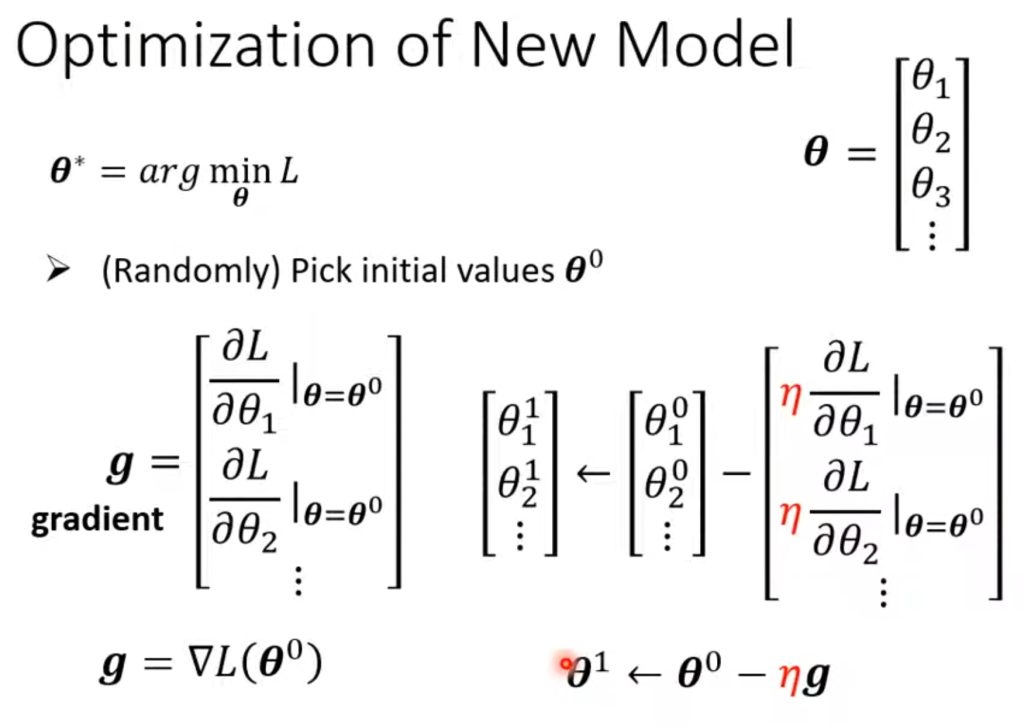
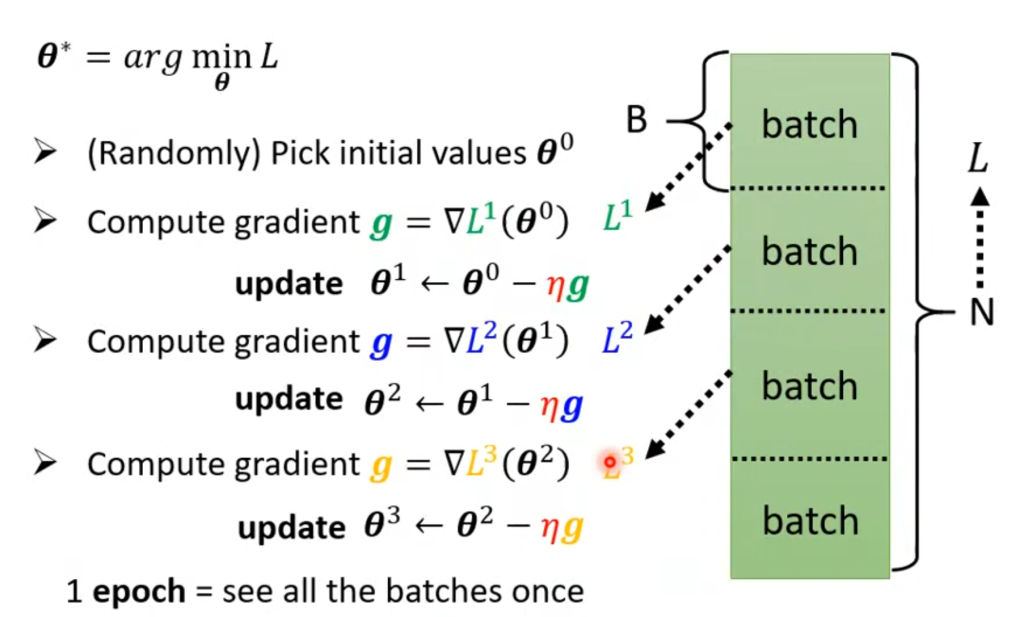
第三步,随机选一个初始点,对所有参数做偏导,偏导集合称为梯度(grandient),一般把求偏导的过程,也就是求梯度的过程写成∇符号。之后进行梯度下降。(图中的θ为参数合集,例如w、b这些)
需要补充的是,机器学习一般不会一口气把所有的数据集N扔进去训练,而是会分成一个个batch(随机分的),然后对每个batch进行梯度下降,最后把所有batch的梯度下降都看完了才算完成一轮训练。其中,一个batch的更新称为update,全部batch都更新完了才称为一个epoch。
补充
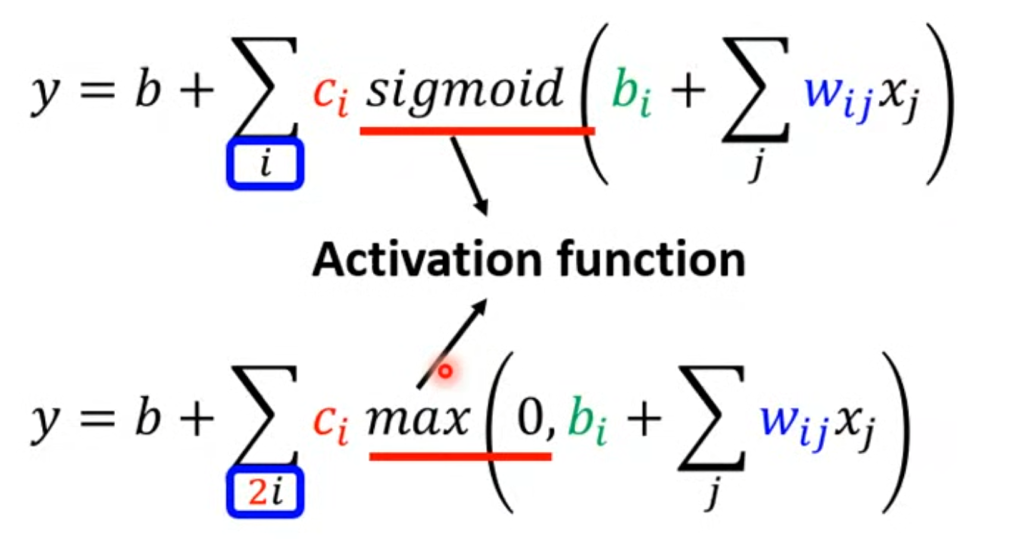
在上面讲到,我们采用若干条标准曲线来构造函数,但并不一定非要用曲线表示,也有折线的专门表达函数
y = c max(0,kx+b),用曲线的表达称为sigmoid,用折线的表达称为relu,二者都为激活函数(activation function)
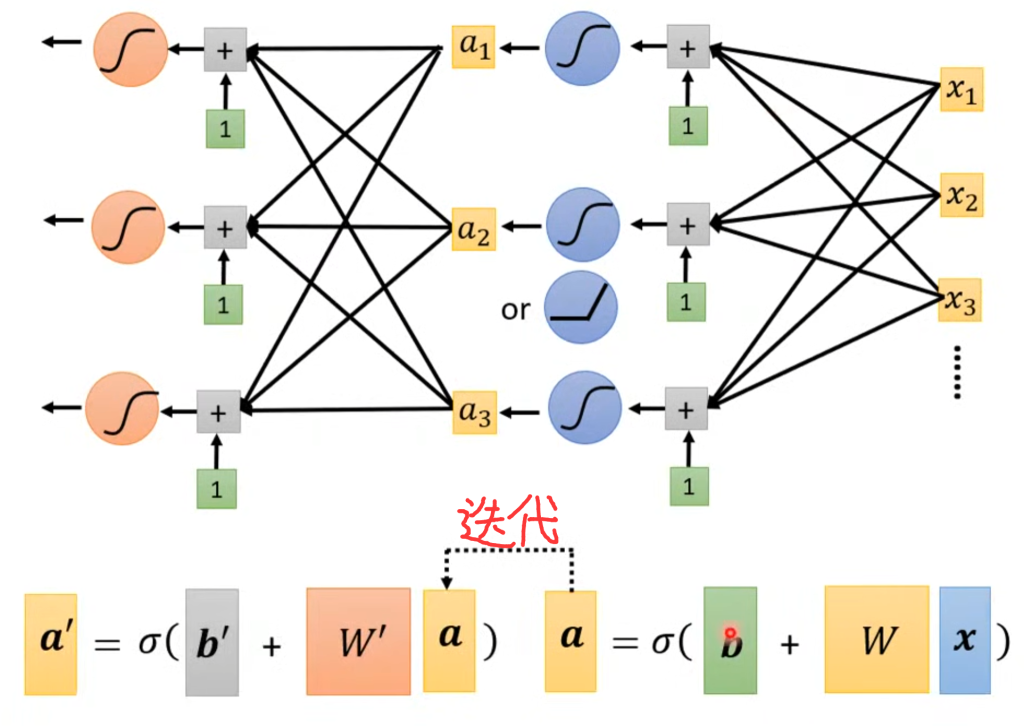
拿sigmoid举例子,假设我们现在有了很多不同的标准曲线(sigmoid),一种增加函数表达能力的方法是让更多不同的标准曲线叠加,这种称为向宽(fat)的方向改进;还有一种是增加函数表达能力的方法是在一个sigmoid后,把这个sigmoid结果当做下一个sigmoid的x继续迭代,这种称为向深度(deep)的方向改进,每一次迭代称为一次layer。但过度layer会使得模型过拟合。具体是fat更好还是deep更好,在后面的章节会说。
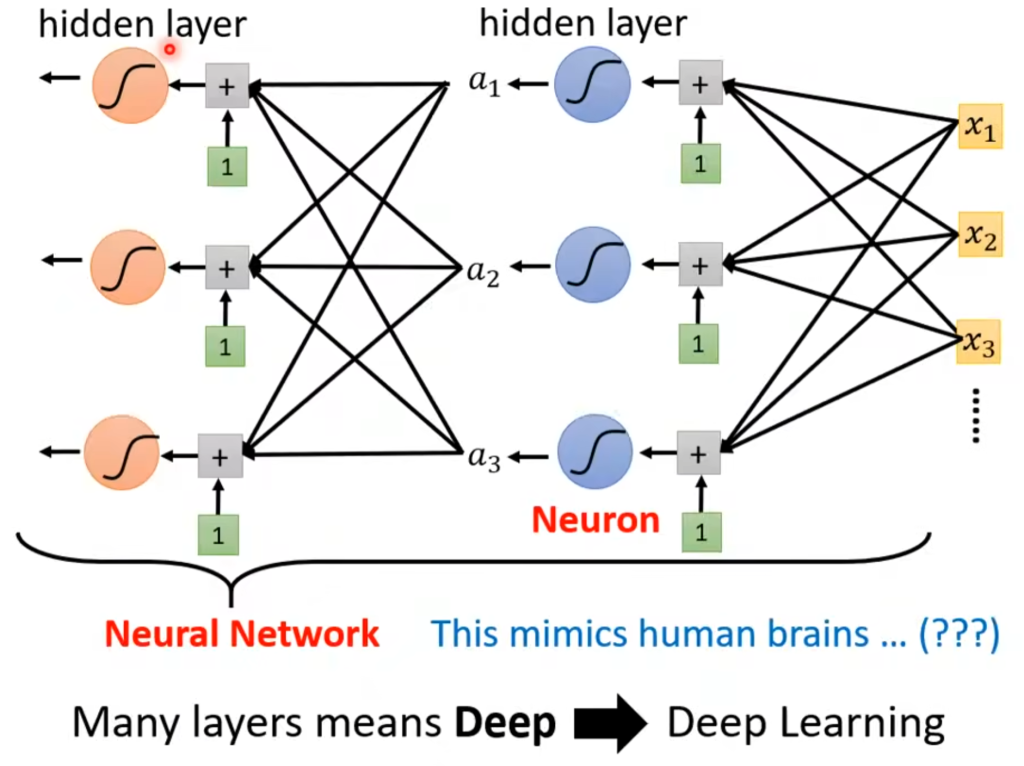
这种sigmoid或者relu被称为神经元(Neuron),整个结构称为神经网络(Neuron Network),但很逆天的是Neuron这个名字在当时已经被用烂了,所以换了一个高端的新名字,即:
一列神经元(Neuron)称为隐含层(hidden layer),很多隐含成被称为Deep,这整套技术就被命名为深度学习(Deep learning)
反向传播
在前面讲到,梯度下降需要计算偏微分,在上面的例子中偏微分还比较好算,但在实际的很多应用中偏微分的计算量是非常大的,为了解决这个问题,引入了反向传播(backpropagation),反向传播并不是另一种训练方法,它只是一种有效率的梯度下降
对于某个神经网络(neural network,简称NN),NN中所有的参数集合为θ,输入数据集x,输出结果为y,它与真实值y拔的差距 | y - y拔 | 设为C,如右图。
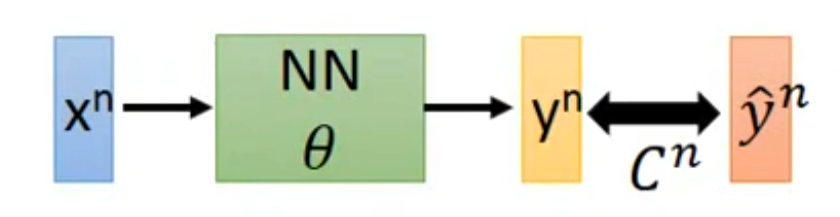
因此整个NN的Loss为C的总和,在梯度下降的时候计算偏微分可以转换为对ΣC的偏微分。
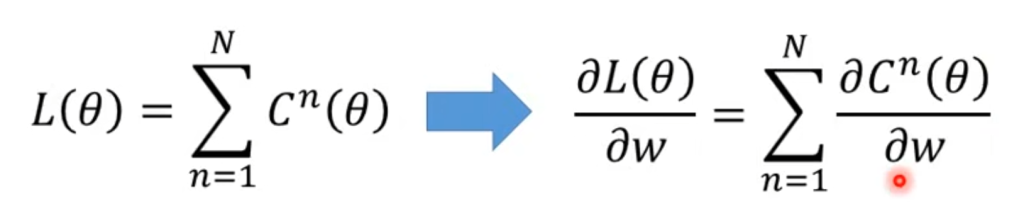
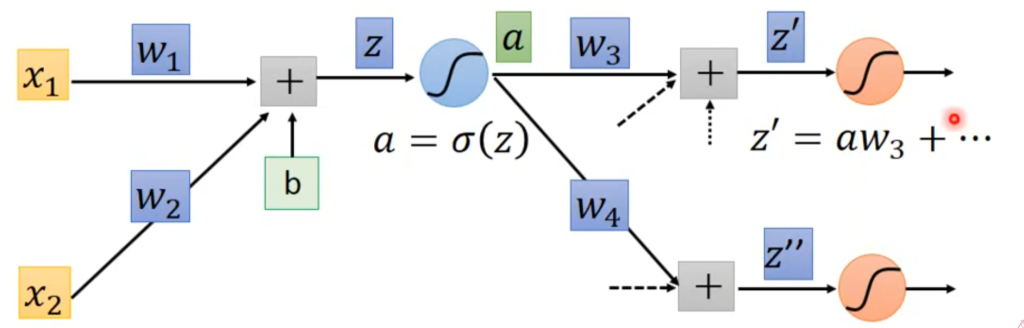
对于某一个神经元,有右图所示的计算过程,
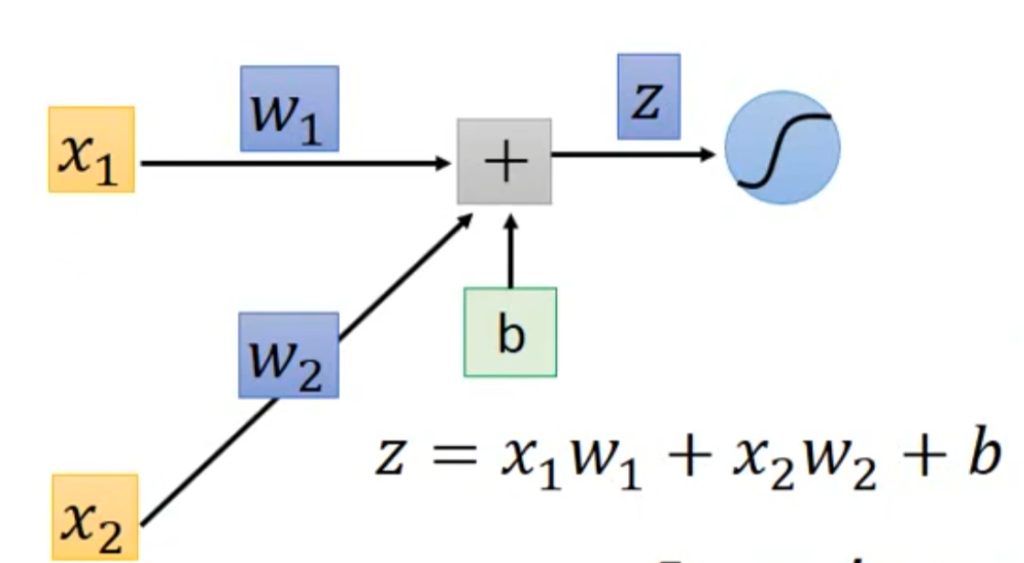
根据链式求导法则,有右图所示推导,其中z对w的偏微分称为forward pass,是好算的,因为z关于w的函数式已知,就是上图所示的式子,问题在于C对z的偏微分比较难求,称为back pass。我们一个一个来
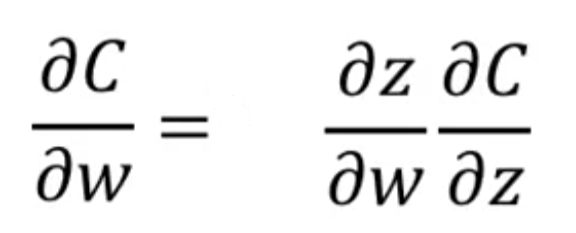
对于z对w的偏微分,就是x。因此可以从NN中快速反应出这个结果,如右图。
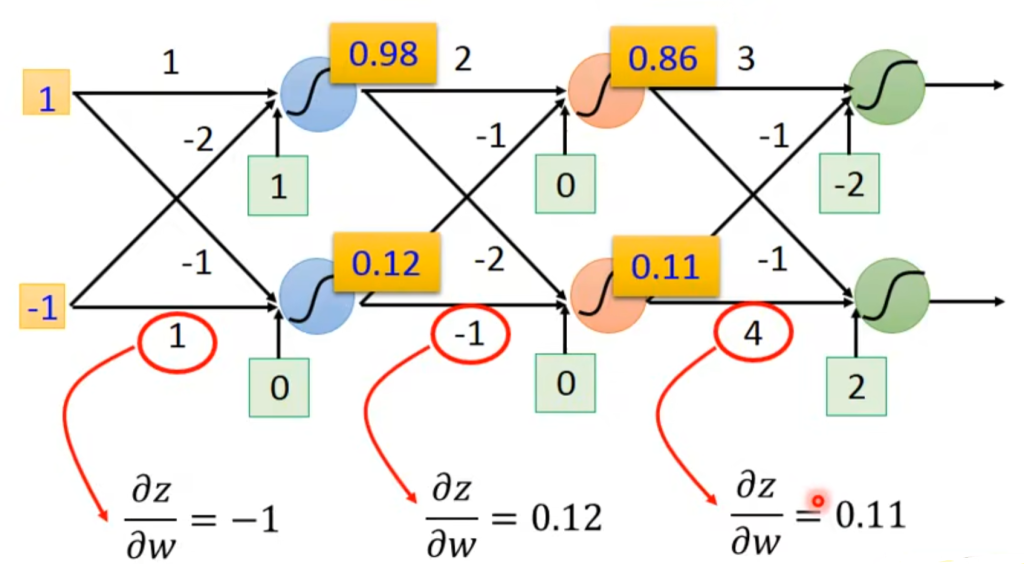
对于C对z的偏微分,可以进一步拆分成这种形式
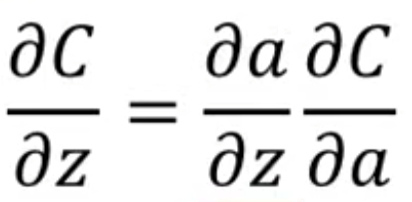
a对z的函数就是sigmoid,是已知的,所以这个偏导也是可以求出来的,如右图
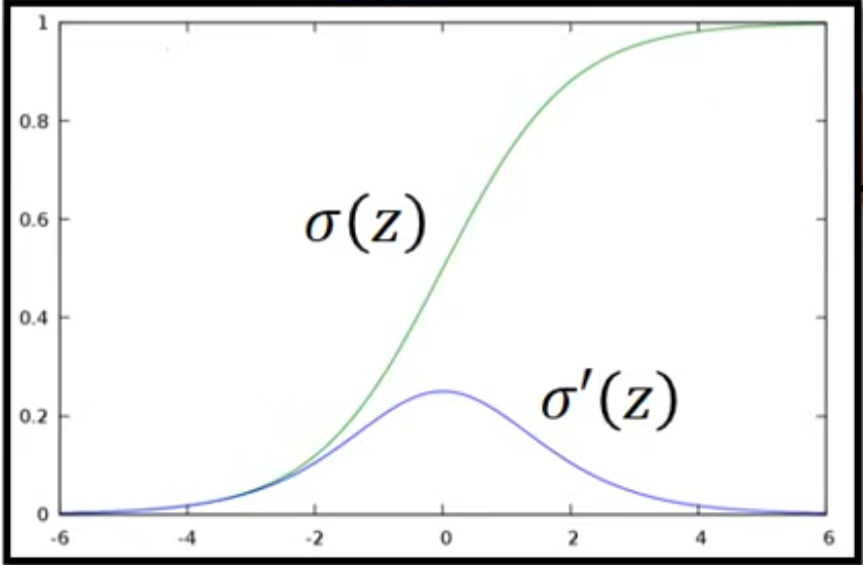
C对a的求导根据后面连接的神经元可以再拆分成右图形式,同理,z对a的偏导好求,C对z的偏导难求。如果后面还有神经元连接那还需要继续拆分,但假如这两个神经元就是最终的输出层,那么根据自己定义的Loss函数,C对z的偏导是能求出来的。
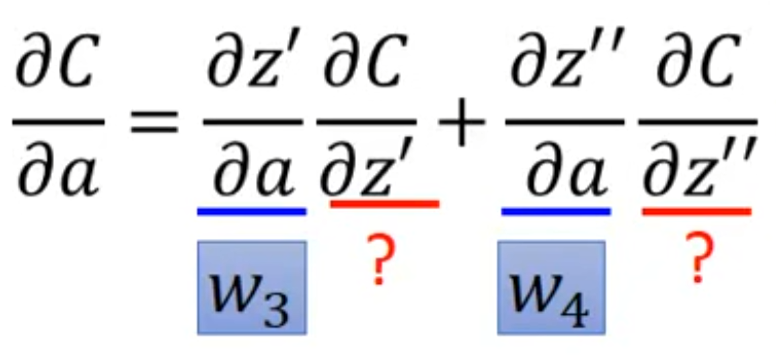
因此假设打问号的这两项是输出层,最终C对z的偏导就可以写成右图该式。如果不是输出层,继续拆分,想要计算就还得知道后面连接的神经元的信息,这看起来很麻烦
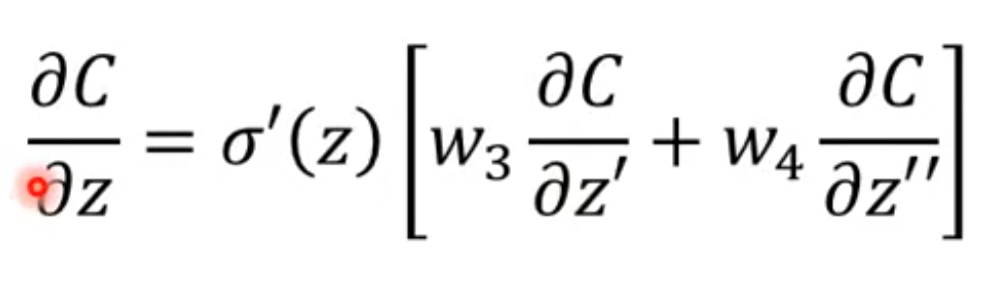
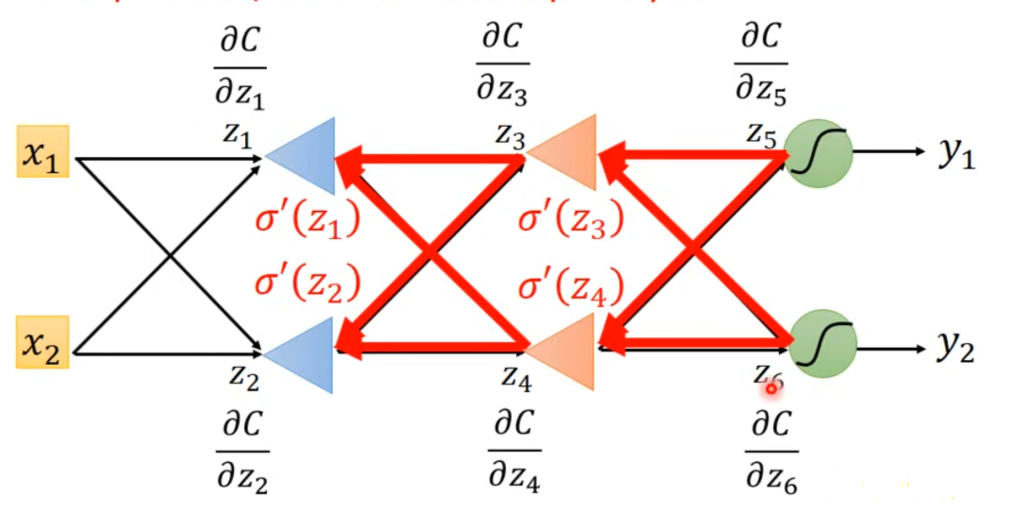
为什么麻烦呢,因为如果你要算z1的偏导,你就得知道z3和z4的偏导,你想知道z3和z4的偏导,你就得知道z5和z6的偏导。因此,反向传播的思想就是在算完forward pass后,直接倒过来求,先求输出层神经元的偏导,这样就可以推出上一层神经元的偏导,以此类推,效率能有极大的提升
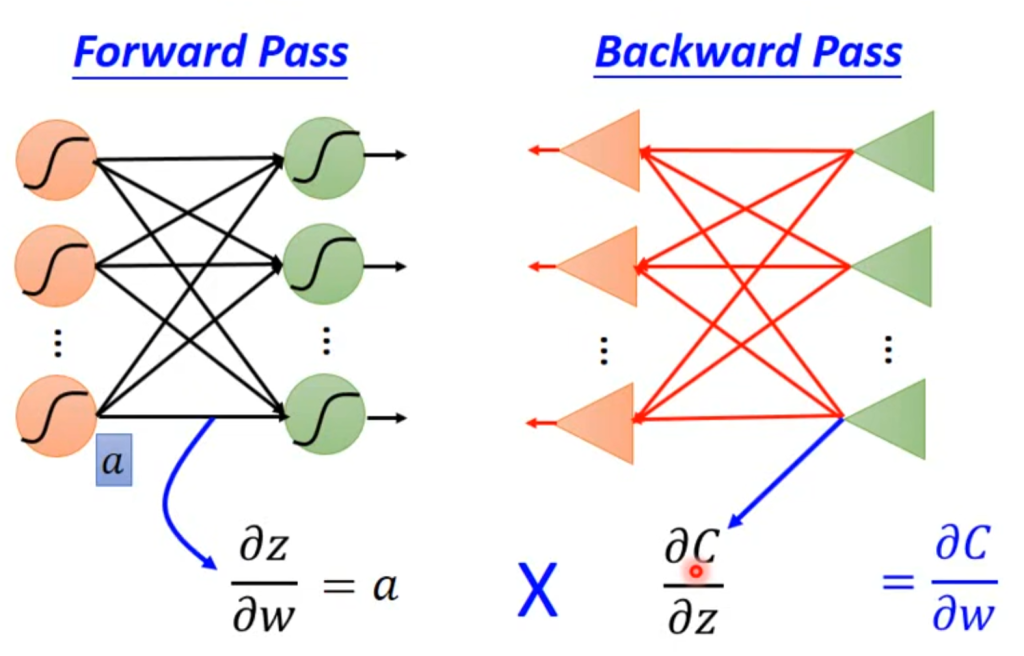
最后总结一下,先通过forward pass求出z对w的偏导,再反向传播求出C对z的偏导,两个相乘,梯度下降的结果就出来了。



Comments NOTHING