机器学习攻略图
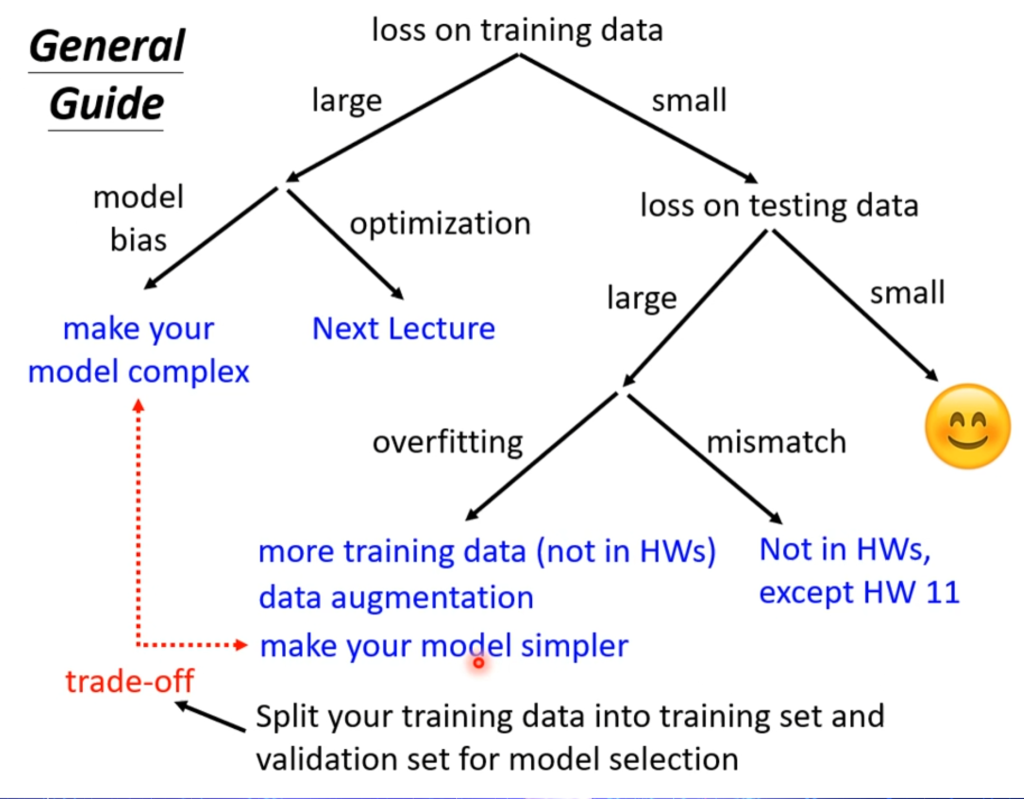
当机器学习训练效果不理想时候,先看在训练集上的损失,如果很大:
模型误差(model bias)
模型误差相当于梯度下降后Loss的值都很大,这时候可能是函数设的太简单了,例如设的是直线但实际上是曲线。打个比方就是在湖里捞针,但针不在湖里。
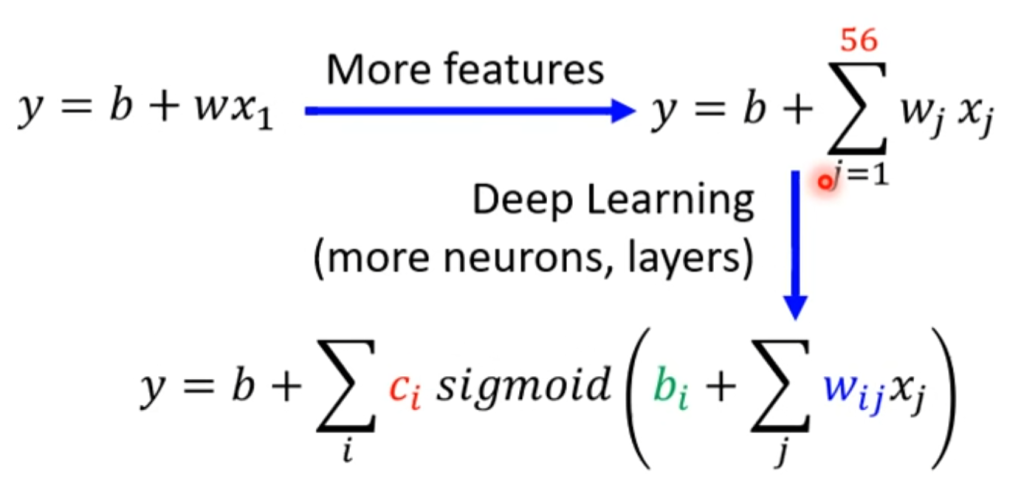
解决办法就是重新设置函数,例如多假如一些特征(流量预测添加前七天的相关性),将liner model变为sigmoid model,或者在深度方面多加几层layer。
优化问题(optimization)
那是否在训练集上Loss大就一定是模型误差呢?不一定,例如上一篇文章提到的非常经典的局部最优和全局最优点的问题,打个比方就是在大海里捞针,针确实在海里,但你方法没用对没找到针。
那么如何判断是模型误差还是优化问题呢?答案是对比多种模型
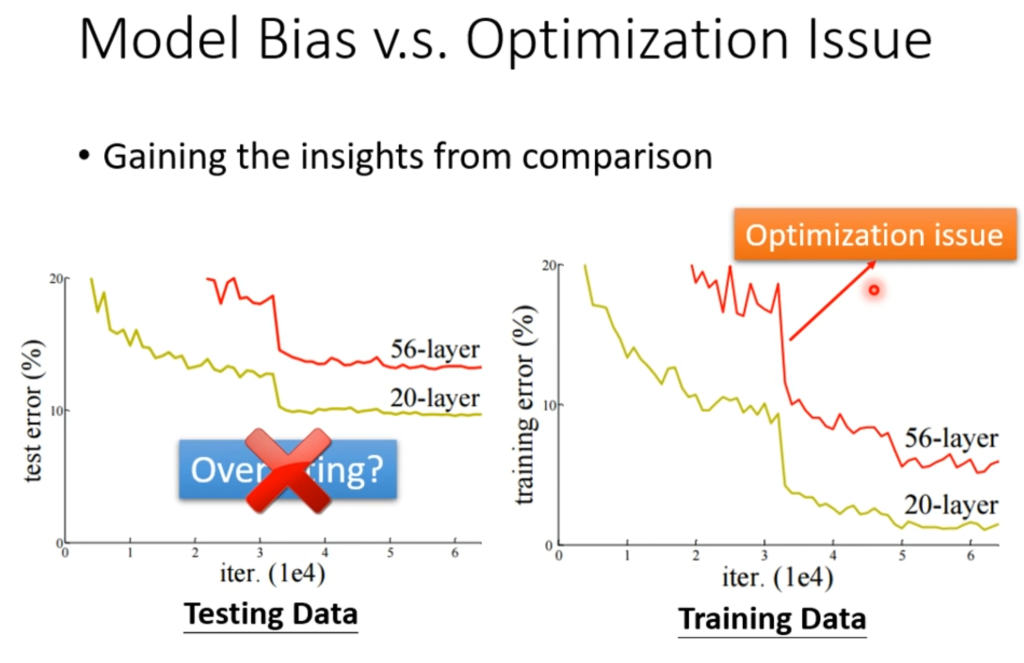
例如上图,在测试集上56层的失误率比20层大不能代表过拟合,要在训练集上看。
在训练集上,56层的模型一定比20层的模型更有弹性,换句话说就是56层的模型包含了20层的模型的,因此56层的最优解一定是比20层的最优解好的,但在训练集上却出现20层比56层好的情况,那这种情况说明56层这个模型的优化没有做好,没有找到最优解。
因此,在遇到训练集上Loss很大的时候,可以再训练一个layer更浅,或者函数更简单的模型,这种简单的模型不太可能出现优化问题,很容易找到自己的最优解,看看在“小”模型上面的Loss是多少,再和复杂模型做对比,以判断是模型误差还是优化问题。
解决办法:下一节会讲。
过拟合(overfitting)
当在训练集上的Loss很小,在测试集上的Loss很大时,有可能发生过拟合。那为什么会发生过拟合呢?一种直观的解释是过拟合就是学习过头了,把训练数据中坏的部分也学进去了,例如下图:
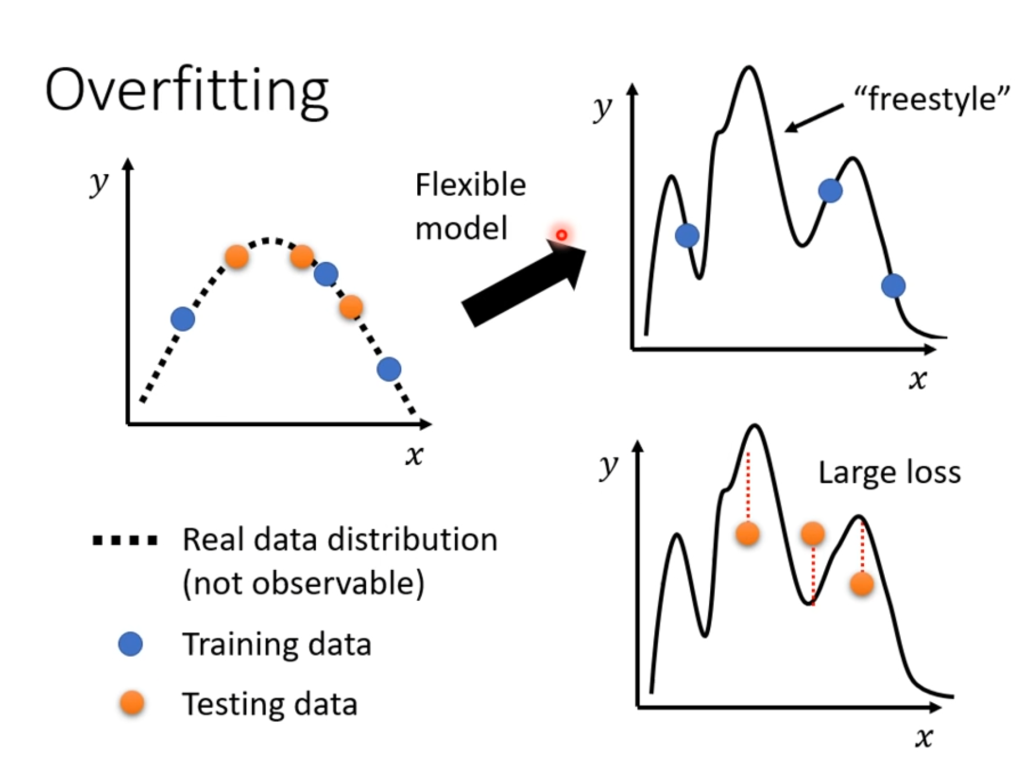
如果训练数据过少(只有三个蓝点),那么机器学习自由发挥的空间就过大了,可能拟合出很乱的模型导致Loss在实际测试下很大。
解决办法:第一种是增加训练数据,减少机器学习自由发挥的空间,第二种是数据扩展(data augmenation),即根据自己的理解将已有数据改造,例如:
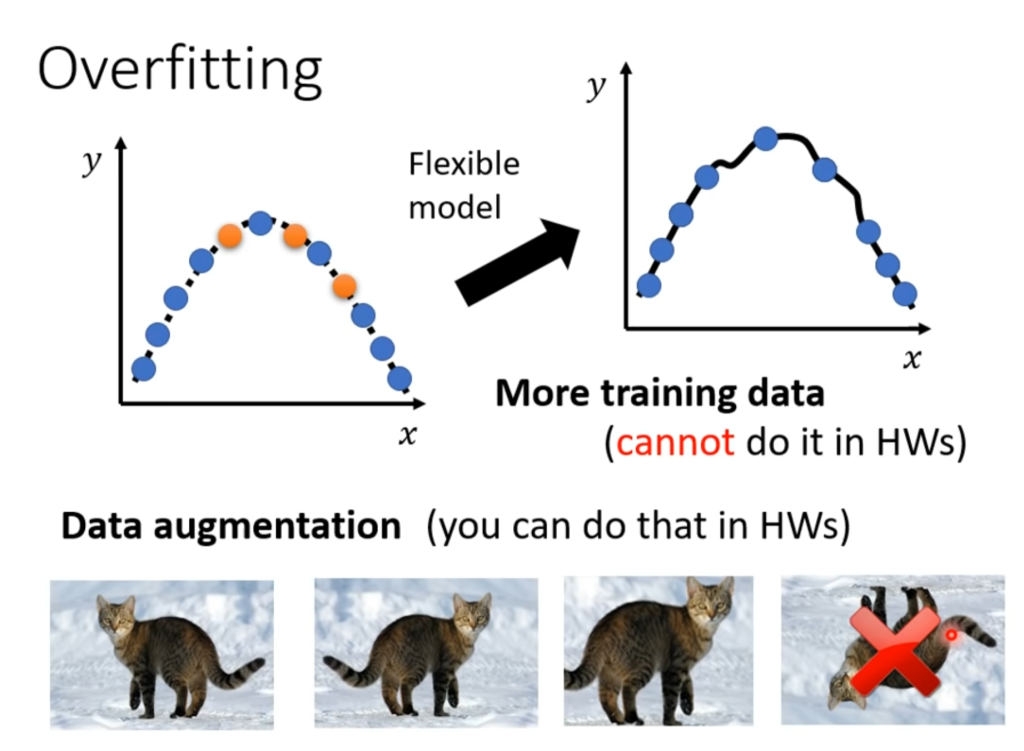
将图片左右调转,局部放大。但不是可以随便改造,例如一个影视图片训练,我们知道在实际看电影的时候不会有上下颠倒的图片,因此如果你改造出了一个上下颠倒的图片会干扰训练,因此数据改造需要具体情况具体考虑。
第二种方法是增加模型的限制,例如你认为实际情况就是二次曲线,那就将模型设为二次函数。除此之外还有减少神经元的数量、共用参数等等,CNN的部分就用到了这个。
因此,一个判断最优解的图像就出现了
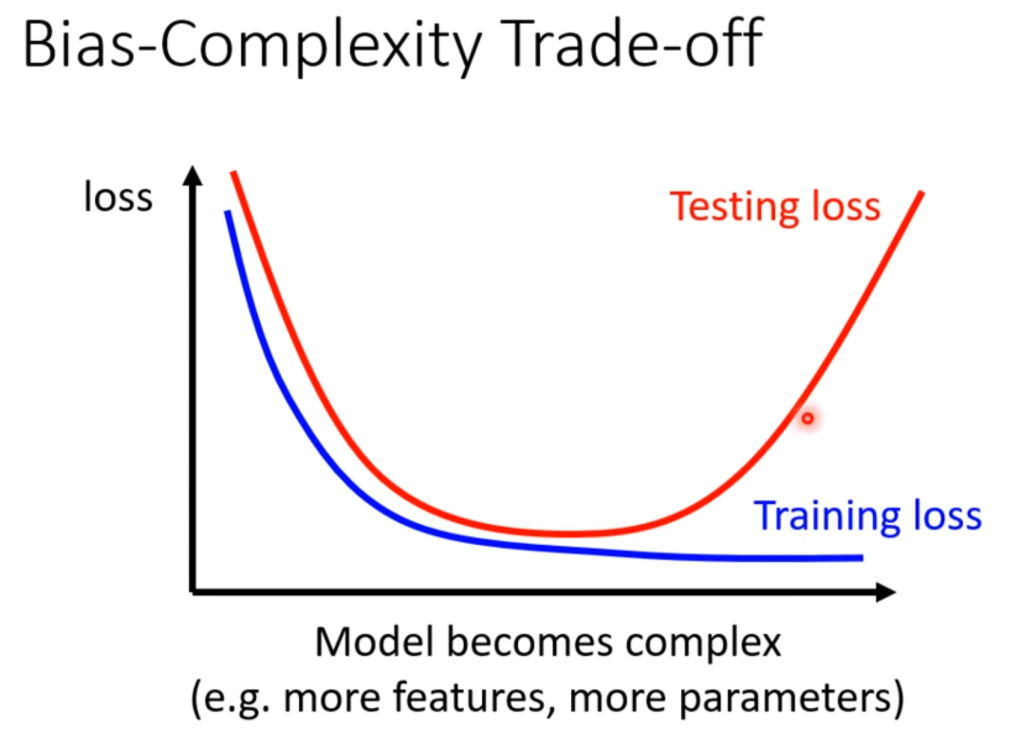
随着模型越来越复杂(特征更多,层数越多),在训练集上的Loss会持续下降,在测试集上的Loss会先将后升,这个升就是过拟合导致的。
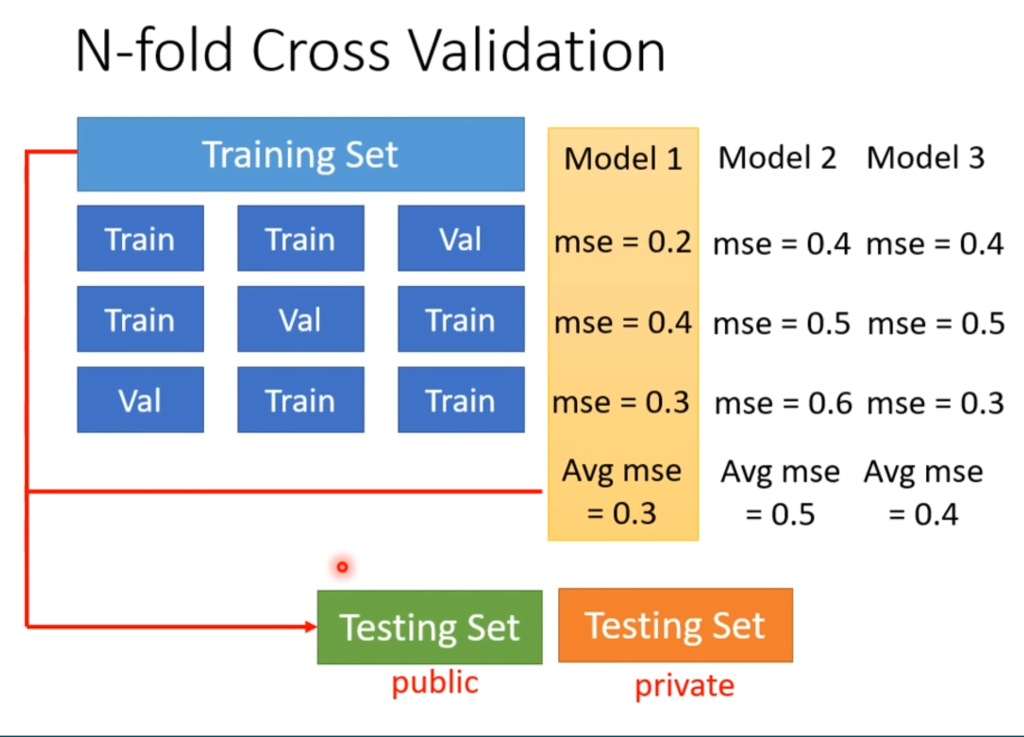
打比赛时候建议的训练方法
将收集到的数据进行N等份,然后依次拿一份作为验证集,并在不同的model上进行训练看Loss,选平均最小的那个提交。
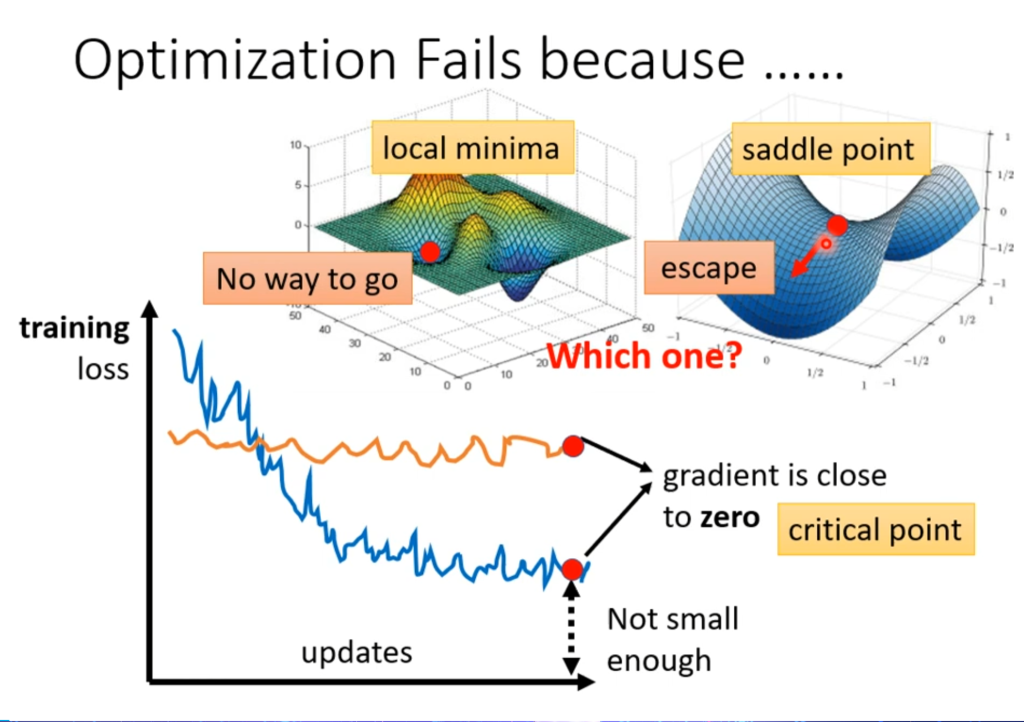
优化问题(optimization)中的局部最小点与鞍点
在上面提到过,当发现是优化问题(没找到最优解)时,可能遇到了两种情况,一种是遇到了局部最小点(local minima),一种是遇到鞍点(saddle point),鞍点的左右高前后低,形状类似马鞍,因此鞍点的偏导也是0。二者统称为临界点(critical point)。
那为什么要弄清临界点是局部最小点还是鞍点呢?因为如果是局部最小解,那确实没有下降的空间了;但如果是鞍点,可以看出还是可以往前后下降,因此还可以继续优化。
如何判断临界点是局部最小点还是鞍点
根据在某一点的泰勒展开,函数可以写成右图的形式,其中g代表一次偏导,H代表二次偏导,如果遇到优化问题,则一次偏导为0,意味着g这一项为0直接不考虑,那么该点的形状就由H这一项决定:
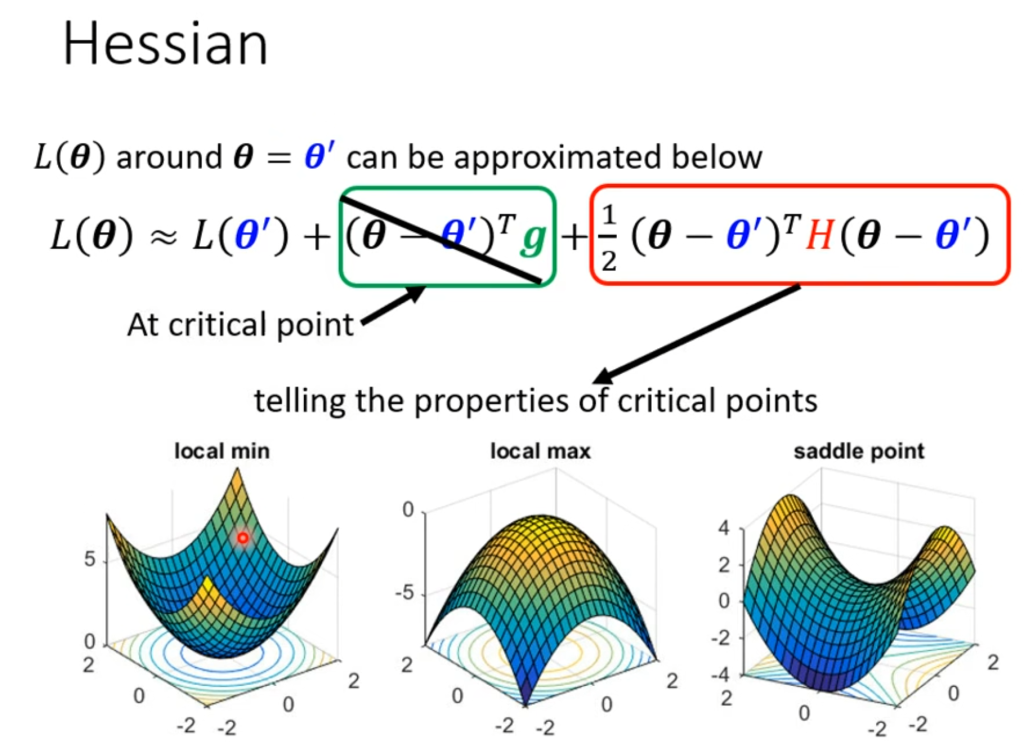
若不管v取何值,该项总是大于0,说明该点是局部最小点。以线代的角度来看即所有特征值都大于0。
若不管v取何值,该项总是小于0,说明该点是局部最高点。以线代的角度来看即所有特征值都小于0.
若当v的取值发生变化时,该项有正有负,说明该点是鞍点。以线代的角度看即特征值有正有负。

当发现鞍点后,找到负特征值对应的特征向量,往这个向量的方向走就可以继续下降。
在实际训练中,参数一般动辄几十上百,因此所有特征值都为正(即局部最小点)的情况非常少见,在偏导为0的点是鞍点的可能性非常大。

batch
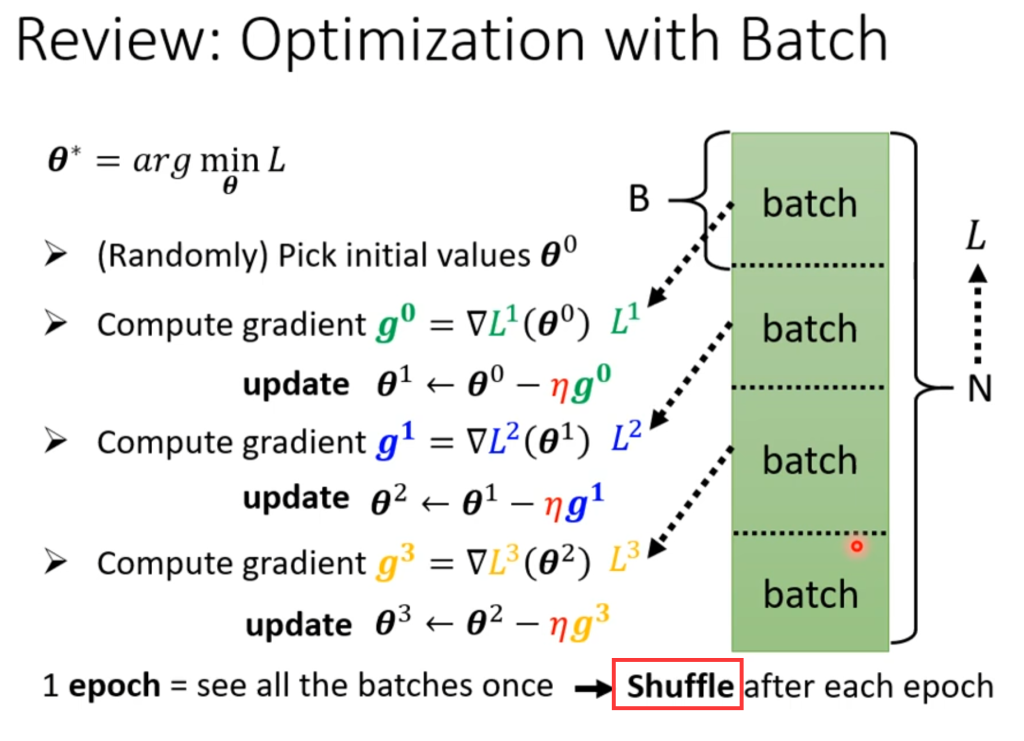
在上一篇文章中讲到,一般训练的时候不会一口气将数据全部扔进去训练,而是分成很多个batch,分开训练,一个batch的更新称为update,全部batch更新完称为一个epoch。
在每一个epoch结束后,下一轮epoch会重新分配batch的大小,叫做shuffle(随机播放)
那么batch的大小定多少比较合适呢?
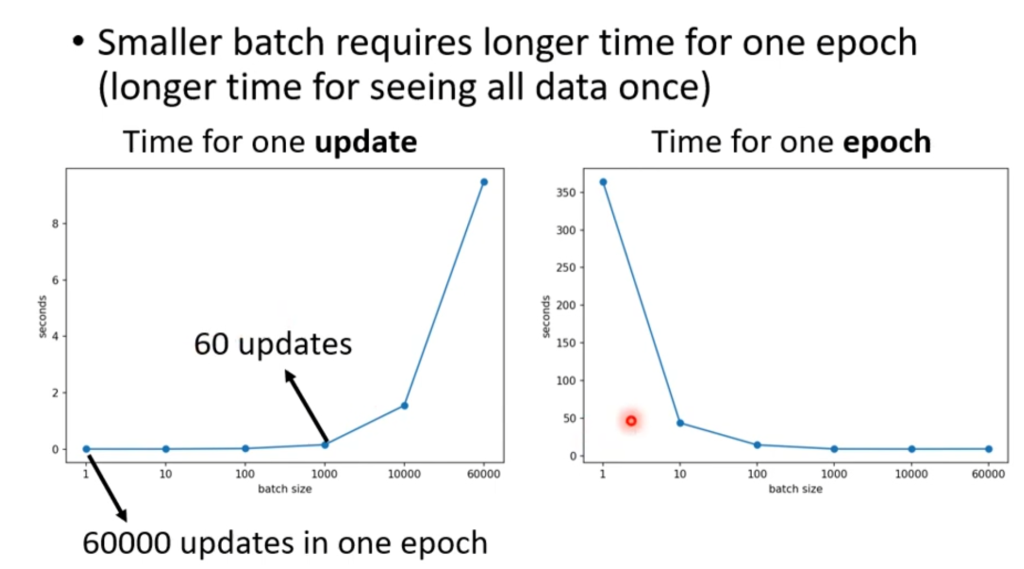
从直觉上来看,如果batch size定满,也就是不切分,花时较长,结果稳定。如果batch size定的很小,花时较短,但每一小步都不是很稳定。

但事实真是如此吗?不一定。
即使一个batch size很大,GPU也可以利用并行运算的功能,将大的batch在短时间内算完。但是如果batch很小,数量就很多,一整轮需要的时间就多了,因此需要花费的总时间为右图所示。
得出的结论是:batch size越大,花费的总时间反而越短。
那么现在看上去batch size大花费的时间少,结果还准确,就没有缺点了吗?不是的。
如果除去时间因素,在实际训练效果上,小的batch size的训练效果反而会更好。直观的解释是,大的batch size分出的数量少,小的batch size分出的数量多,因此在一条路走不通的时候,去另一条路可能就走通了。
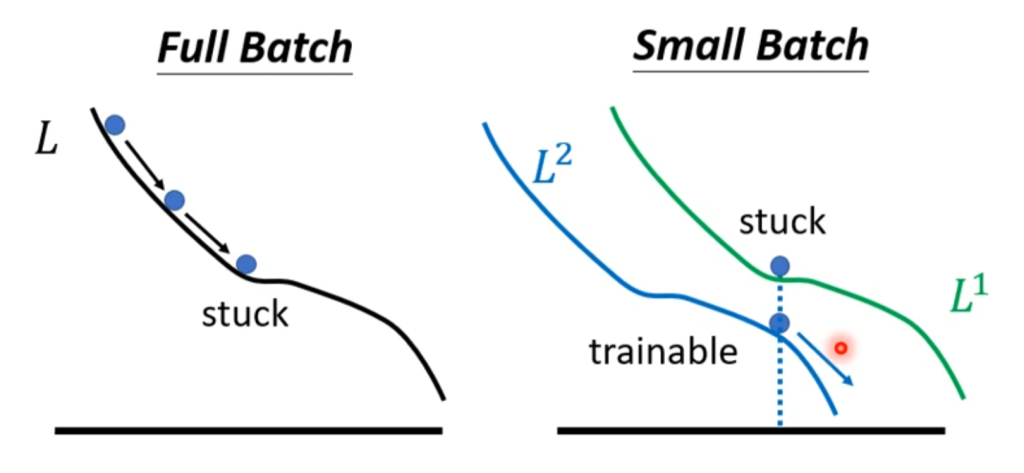
总结一下,小的batch size优化更好,测试也更好。大的batch size花费的时间更短,因此实际训练中batch size的取值也是我们需要手动设置的一个超参数。
Momentun
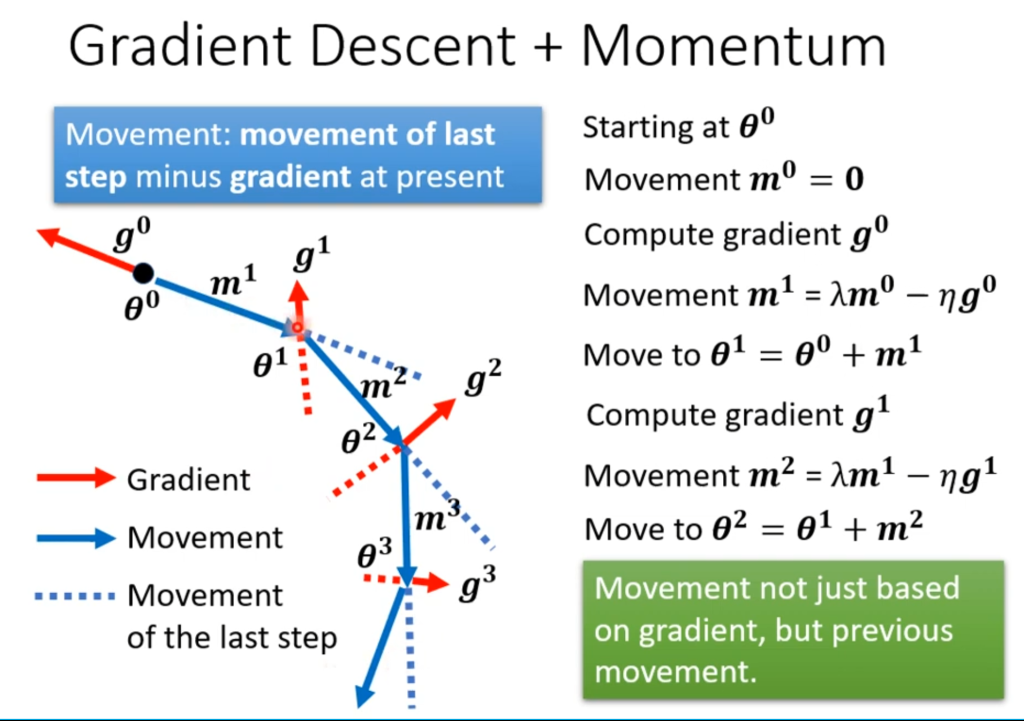
Momentun技术是在优化过程中使用的另一种方法,其原理可以类比现实中的小球滚下山丘:当小球滚到局部最低点的时候并不会立刻停下,而是会由于惯性继续前进一小段距离,若这一小段距离足以翻越山丘,他就会继续寻找下一个局部最低点,结果可能会比上一个局部最低点更好。
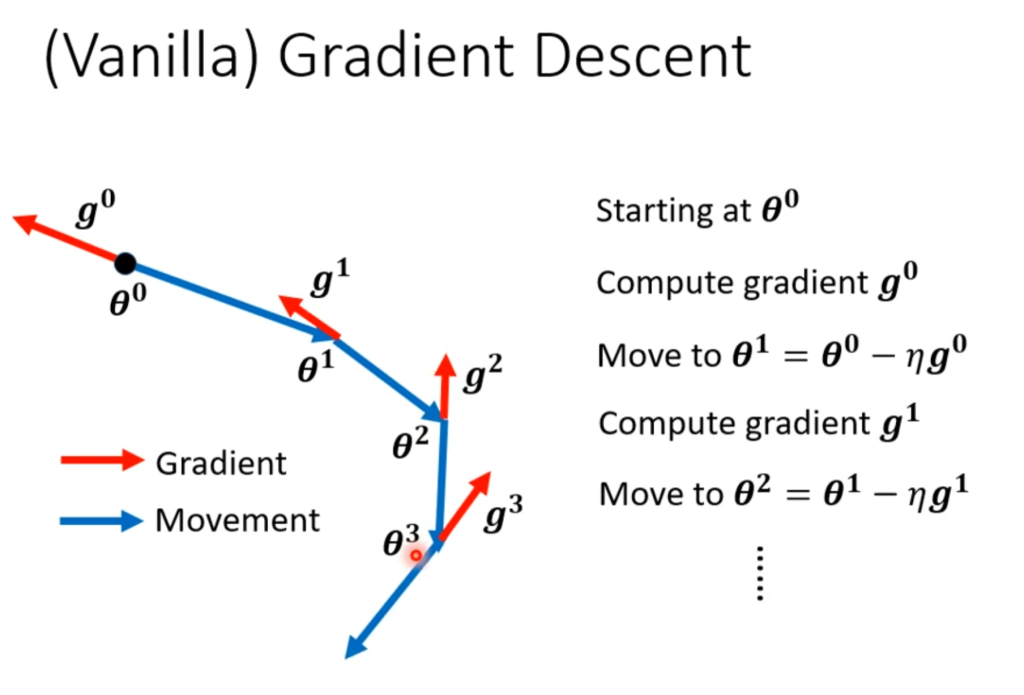
在不使用Momentun技术时,梯度下降的过程如右图所示,会一直往当前偏导的反方向前进(下降)。
在使用了Momentun技术后,梯度下降的过程如右图所示,前进的方向由偏导和上一次前进的方向共同决定。
为每个参数自动赋值学习率(learning rate)
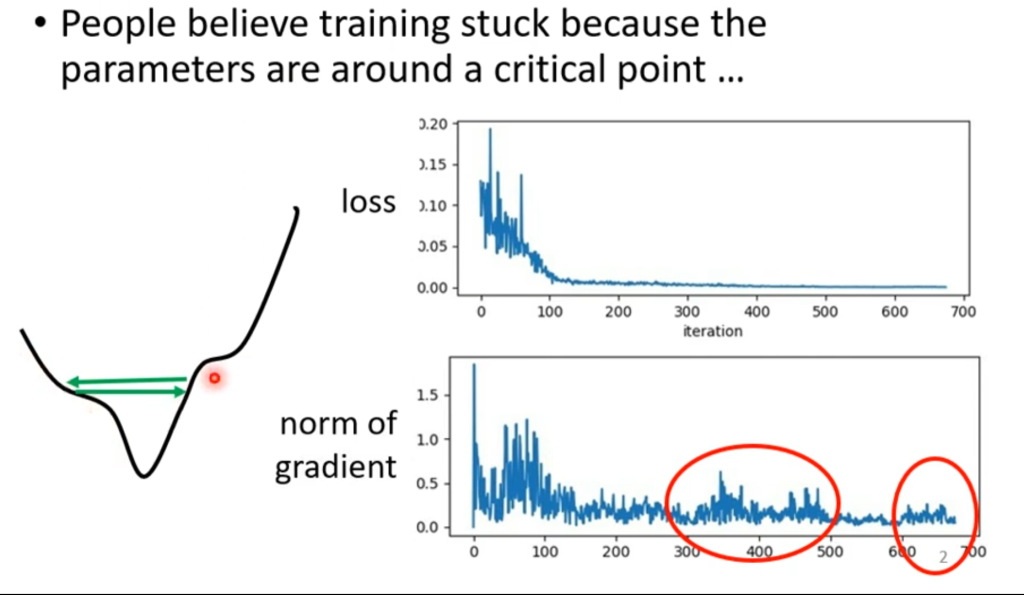
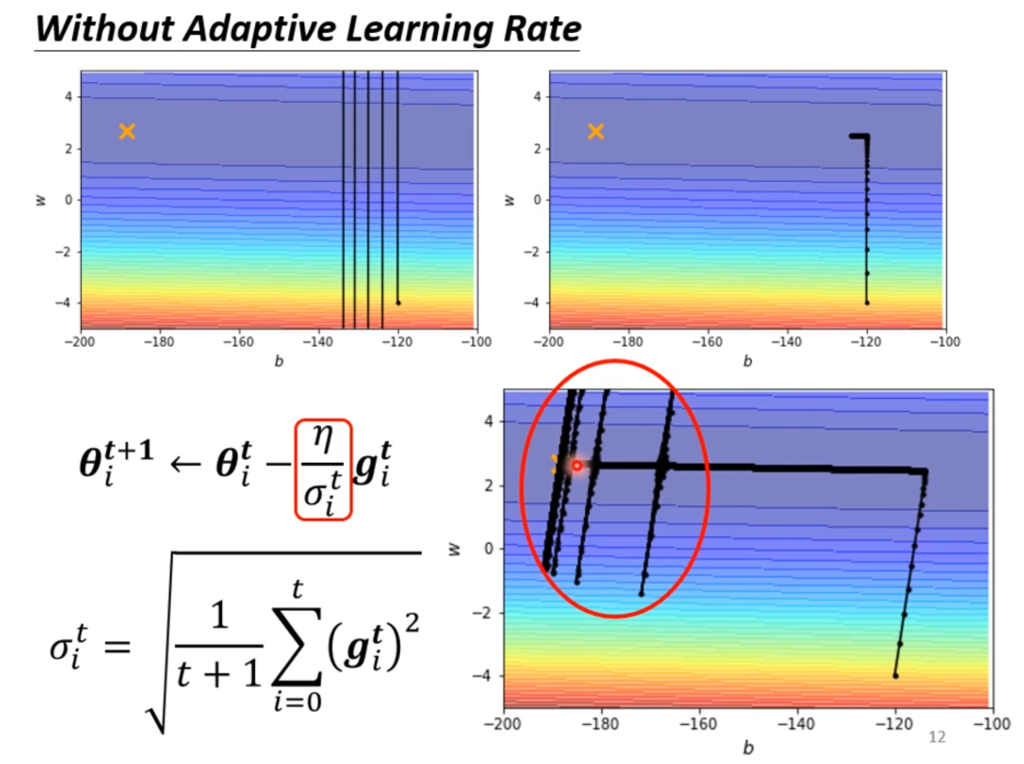
在机器学习的训练中,临界点(critical point)并不是最大的难题。我们知道当Loss下降到基本稳定的时候就是已经达到临界点了,但事实真的是这样吗?从下图就可以看出来,如果学习率很大,会导致跨的步子太大,从而在山谷之间徘徊从而无法掉下去,此时并没有到达临界点。
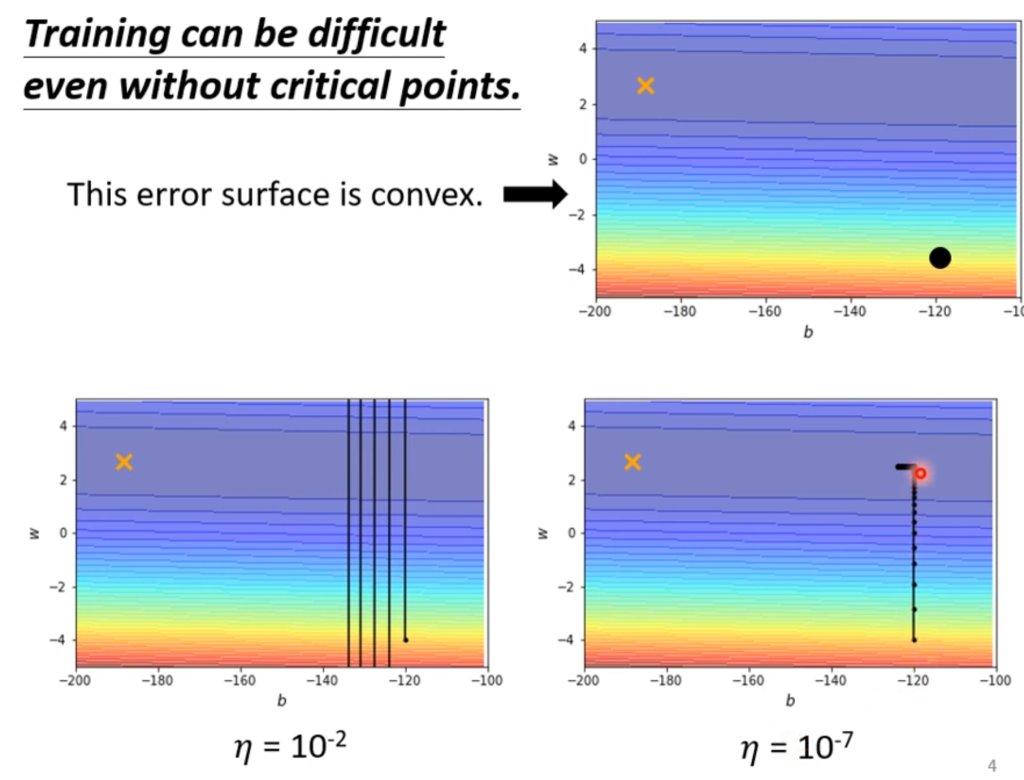
举一个例子,图中的x为最优点,出发点是黑点。如果学习率设置过大,则会出现上述在山谷里徘徊无法掉下去的情况,如果学习率设置太小,则会导致掉落的速度非常缓慢(图中左拐后已经经过了10000次更新才走过一小段距离)
因此,自动根据不同参数调整对应的学习率这个优化方案就被提出来了。我们希望坡度比较大时,学习率小(步子小);坡度比较小时,学习率大(步子大)。
如右图,原来直接用学习率η和参数相乘,现在用η/σ代替,这个σ将会随着参数的变化而变化。
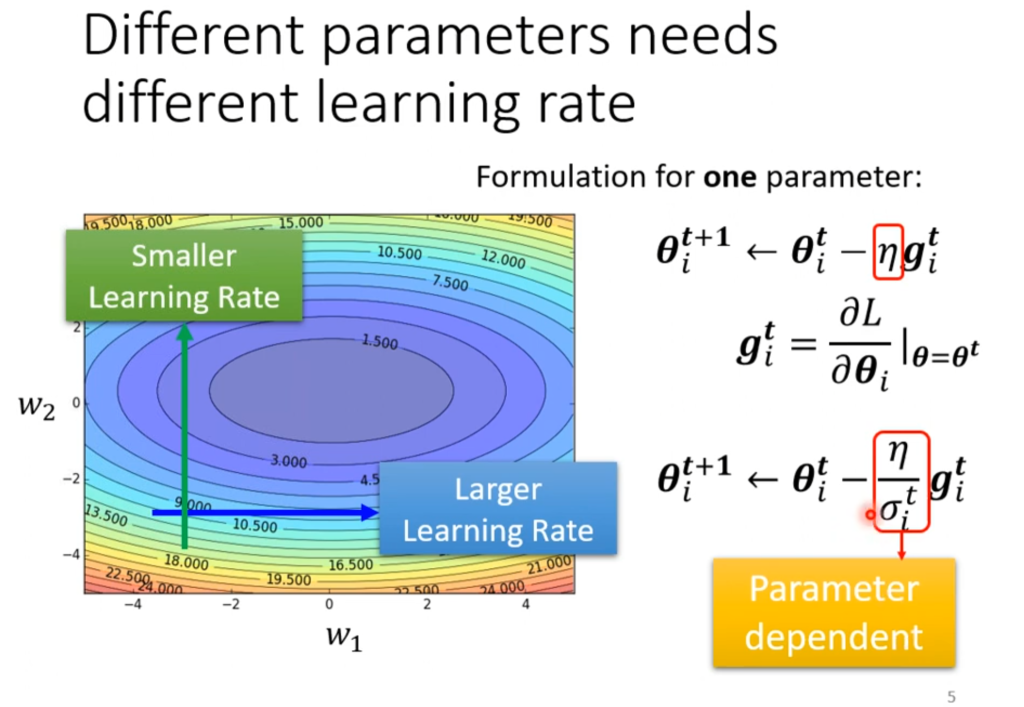
那么这个σ如何设置呢,一种常见的设法为均方根值(root mean square)。均方值可以让坡度大的时候学习率变小,在坡度小的时候学习率变大。
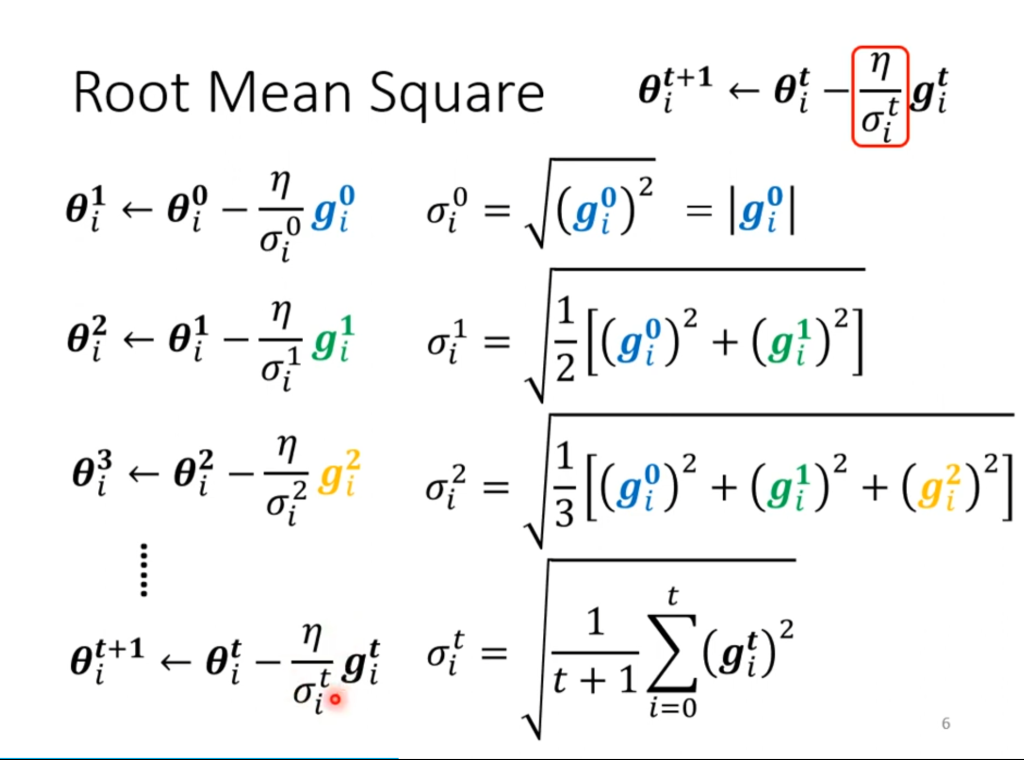
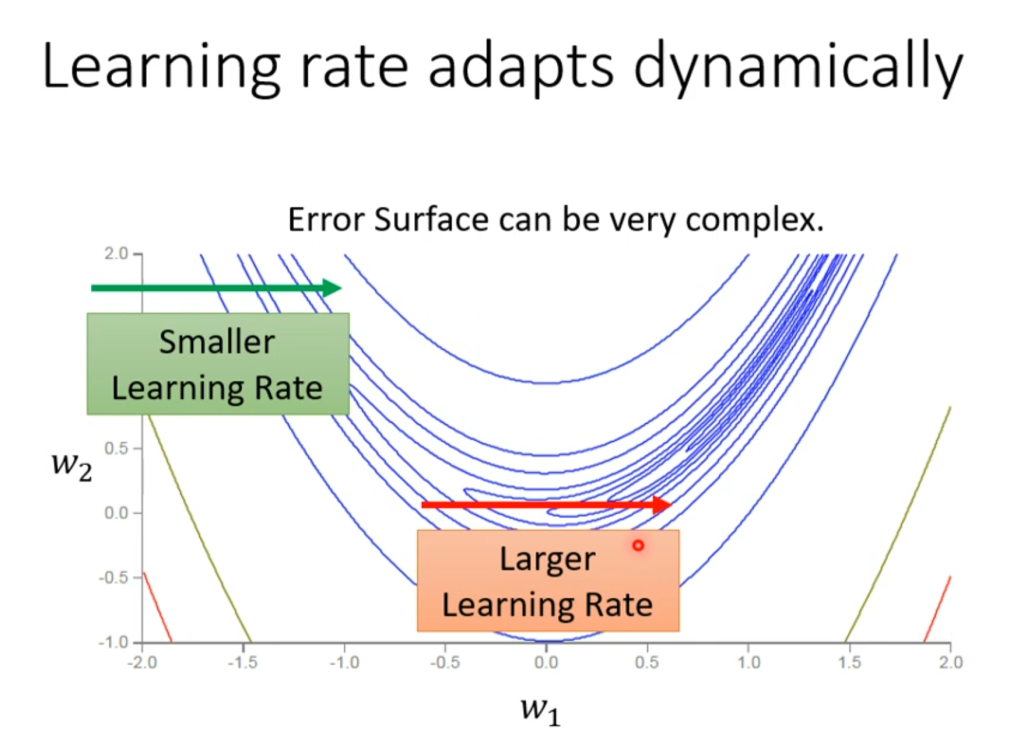
当然,这并不是最终的解决方案。如右图,即使是同一个参数,也有可能遇到坡度大和坡度小的都会出现的情况。因此,同一个参数也能动态的调整参数才是最终想要的。
最终的方法为RMS。它和均方差不同的地方在于,对于每一个σ,都有一个α决定刚算出来的g对这次有多重要。
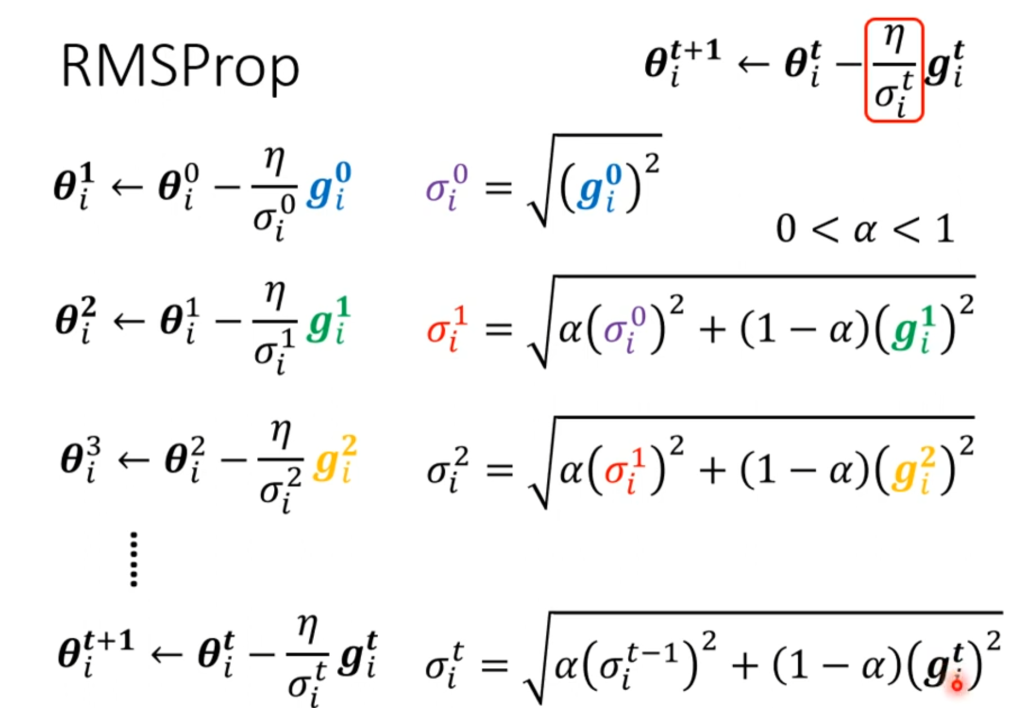
learning rate schedule
在有了自动调整参数的学习率后,训练过程会变成什么样呢?如右图,在拐弯之后确实可以大步子迈向终点了,但在靠近终点的地方突然爆炸,这是因为在拐弯之后的σ值都很小,积累下来导致步子又突然变大了。当然也没事,因为喷出去之后σ又变大了,后面会慢慢回来。
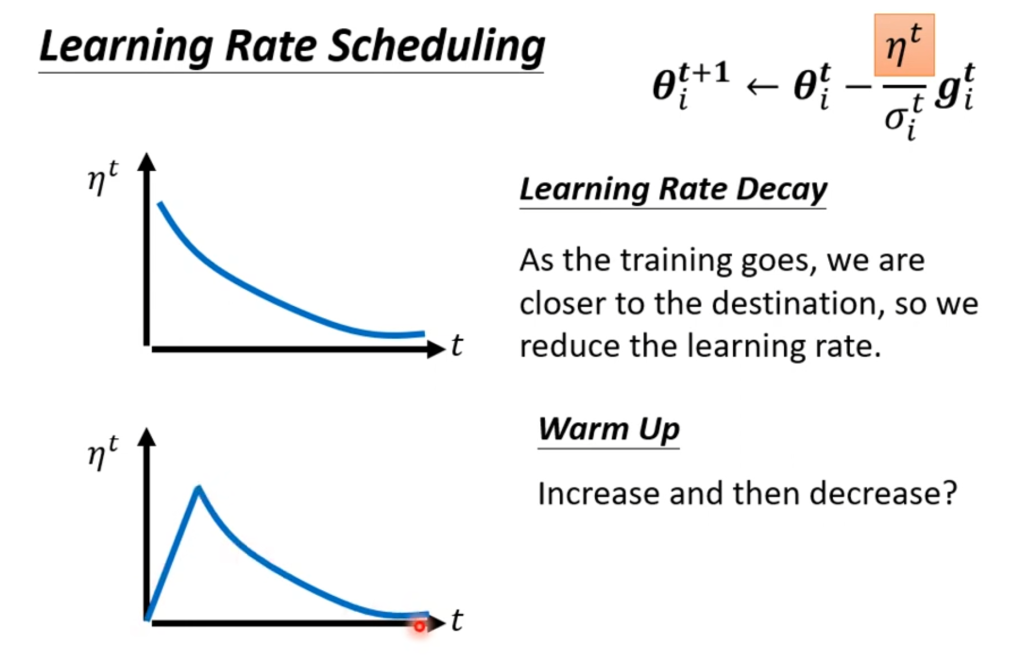
而解决这个问题的就是learning rate schedule,将η调整为一个随着时间变化而变化的量
一个常用的变化为learning rate decay,即随着时间变化慢慢减小,这样到靠近终点的时候就不会突然喷出去了。
另一个偶尔用到的变化为warm up,这算一种“黑科技”,大致趋势是先增后减,通俗的讲就是现在出发点附近探索一下,然后再出发,在某些领域有奇效。
总结
那么优化问题就讲完了,总结一下:原本用的是普通的梯度下降,在用了momentun(惯性),自动赋值学习率,learning rate schedule后,可以更快更准确的找到终点。
当然这些并不需要非常清楚原理,这三个优化方案pytorch都打包好了,用几行代码就可以实现了,主要还是对原理的理解。




Comments NOTHING