liner model
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0] # 存数据集
y_data = [2.0, 4.0, 6.0]
def forward(x): # 定义函数(机器学习三步走的第一步)
return x * w
def loss(x, y): # 定义loss函数
y_pred = forward(x)
return (y_pred - y) ** 2
# 穷举法
w_list = [] # 因为要存放权值和对应的loss,所以先开一个容器
mse_list = []
for w in np.arange(0.0, 4.1, 0.1): # range左闭右开,步长为0.1,因此列出了从0到4的所有数
print("w=", w)
l_sum = 0
for x_val, y_val in zip(x_data, y_data): # zip函数将两个数组压缩成一个二维数组
y_pred_val = forward(x_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
print('\t', x_val, y_val, y_pred_val, loss_val)
print('MSE=', l_sum / 3)
w_list.append(w) # 向之前提前开的俩容器中依次加入w和loss
mse_list.append(l_sum / 3) # 别忘了这是MSE,所以要除以n
plt.plot(w_list, mse_list) # 第一个是横坐标,第二个是纵坐标
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()
部分输出:
w= 0.0
1.0 2.0 0.0 4.0
2.0 4.0 0.0 16.0
3.0 6.0 0.0 36.0
MSE= 18.666666666666668
w= 0.1
1.0 2.0 0.1 3.61
2.0 4.0 0.2 14.44
3.0 6.0 0.30000000000000004 32.49
MSE= 16.846666666666668
w= 0.2
1.0 2.0 0.2 3.24
2.0 4.0 0.4 12.96
3.0 6.0 0.6000000000000001 29.160000000000004
MSE= 15.120000000000003
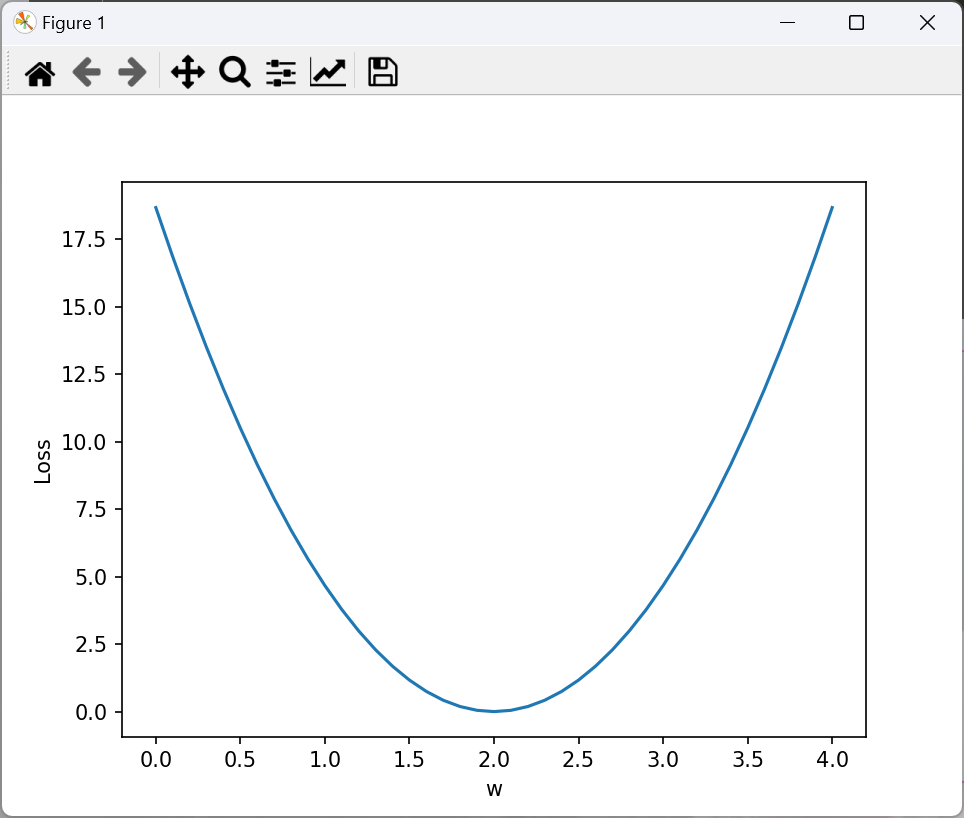
可以看到取w=2时,loss最小。
梯度下降
import matplotlib.pyplot as plt
# 训练集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 初始值的设置,随便设
w = 1.0
# 第一步,定义函数
def forward(x):
return x*w
# 总loss的函数
def cost(xs, ys):
cost = 0
for x, y in zip(xs,ys):
y_pred = forward(x)
cost += (y_pred - y)**2
return cost / len(xs)
# 算梯度的函数,也就是偏导
def gradient(xs,ys):
grad = 0
for x, y in zip(xs,ys):
grad += 2*x*(x*w - y)
return grad / len(xs)
epoch_list = [] # 用来存轮数和对应的cost
cost_list = []
print('predict (before training)', 4, forward(4)) #我们看看在训练之前,如果输入4会输出什么,此时w=1
for epoch in range(100): # 训练一百轮
cost_val = cost(x_data, y_data)
grad_val = gradient(x_data, y_data)
w-= 0.01 * grad_val # 0.01 learning rate
print('epoch:', epoch, 'w=', w, 'loss=', cost_val)
epoch_list.append(epoch)
cost_list.append(cost_val)
print('predict (after training)', 4, forward(4)) # 我们看看训练后,w的值改变了,这时候输入4会输出什么。
plt.plot(epoch_list,cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()
predict (before training) 4 4.0
epoch: 0 w= 1.0933333333333333 loss= 4.666666666666667
epoch: 1 w= 1.1779555555555554 loss= 3.8362074074074086
epoch: 2 w= 1.2546797037037036 loss= 3.1535329869958857
epoch: 3 w= 1.3242429313580246 loss= 2.592344272332262
…….
epoch: 97 w= 1.9999324119941766 loss= 2.593287985380858e-08
epoch: 98 w= 1.9999387202080534 loss= 2.131797981222471e-08
epoch: 99 w= 1.9999444396553017 loss= 1.752432687141379e-08
predict (after training) 4 7.999777758621207
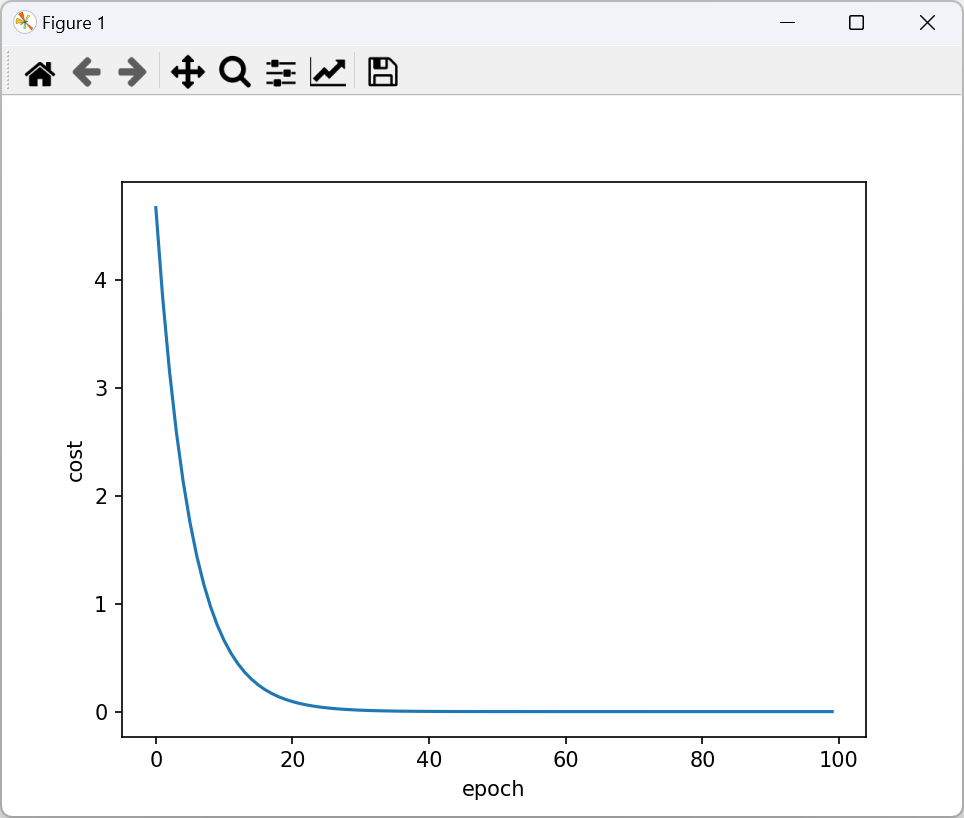
这个是把训练集一次性全扔进去训练,也就是把batch的值调的最大,这种方法在理论篇中提到过,可以减少训练时间。但如果一个一个扔进去训练,也就是令batch = 1。那么训练时间会变长,训练的loss很可能会更低。因此,使用batch=1 的训练过程为:
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0
def forward(x):
return x * w
# 这里改为只计算一步的loss
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
# 偏导也相对应的修改
def gradient(x, y):
return 2 * x * (x * w - y)
epoch_list = []
loss_list = []
print('predict (before training)', 4, forward(4))
for epoch in range(100):
for x, y in zip(x_data, y_data):
grad = gradient(x, y)
w = w - 0.01 * grad
print("\tgrad:", x, y, grad)
l = loss(x, y)
print("progress:", epoch, "w=", w, "loss=", l)
epoch_list.append(epoch)
loss_list.append(l)
print('predict (after training)', 4, forward(4))
plt.plot(epoch_list, loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()
predict (before training) 4 4.0
grad: 1.0 2.0 -2.0
grad: 2.0 4.0 -7.84
grad: 3.0 6.0 -16.2288
progress: 0 w= 1.260688 loss= 4.919240100095999
grad: 1.0 2.0 -1.478624
grad: 2.0 4.0 -5.796206079999999
grad: 3.0 6.0 -11.998146585599997
progress: 1 w= 1.453417766656 loss= 2.688769240265834
grad: 1.0 2.0 -1.093164466688
grad: 2.0 4.0 -4.285204709416961
grad: 3.0 6.0 -8.87037374849311
….
progress: 98 w= 1.9999999999998967 loss= 9.608404711682446e-26
grad: 1.0 2.0 -2.0650148258027912e-13
grad: 2.0 4.0 -8.100187187665142e-13
grad: 3.0 6.0 -1.6786572132332367e-12
progress: 99 w= 1.9999999999999236 loss= 5.250973729513143e-26
predict (after training) 4 7.9999999999996945
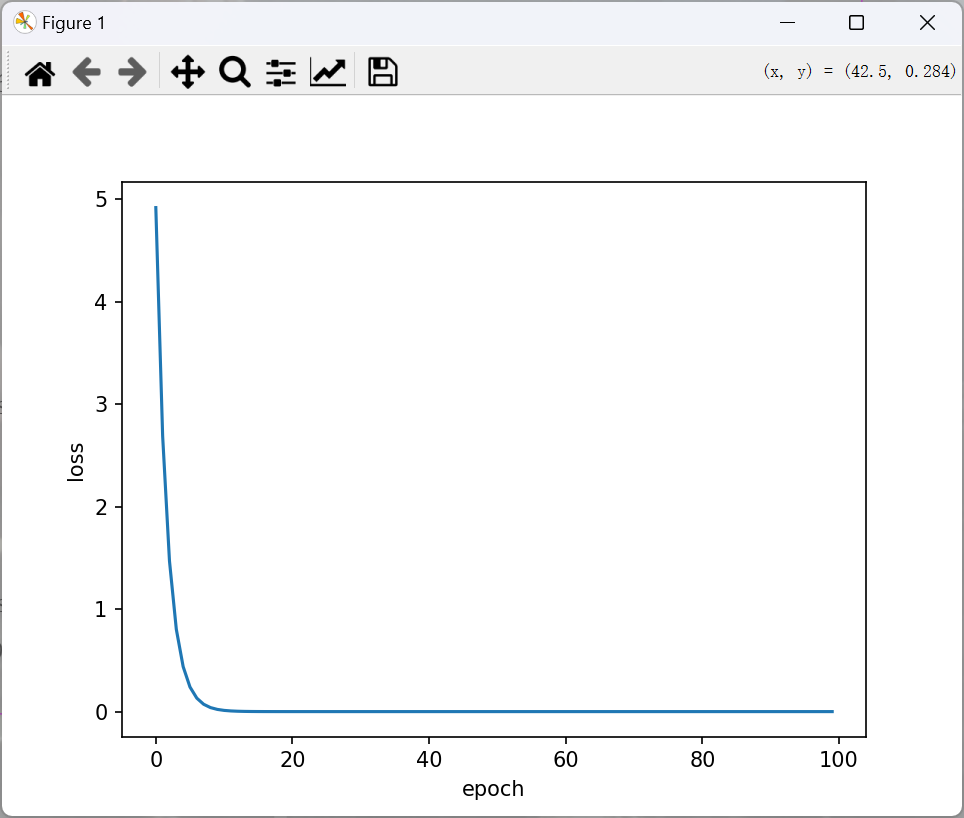
反向传播
首先介绍一下,接下来要用到一种数据类型叫tensor(张量类型),例如令w = torch.tensor([1.0]),w就是tensor类型,包括两个部分,分别是data和grad,w.data和w.grad的类型也是tensor。grad的初始值为None,表示用tensor类型运算的时候不需要计算梯度。而更新w.data的时候要对标量更新而不是张量,所以要用w.grad.data。
接下来是tensor相关的类型。
import torch
a = torch.tensor([1.0])
a.requires_grad = True # 或者 a.requires_grad_()
print(a)
print(a.data)
print(a.type()) # a的类型是tensor
print(a.data.type()) # a.data的类型是tensor
print(a.grad)
print(type(a.grad))
tensor([1.], requires_grad=True)
tensor([1.])
torch.FloatTensor
torch.FloatTensor
None
<class ‘NoneType’>
import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = torch.tensor([1.0]) # w的初值为1.0
w.requires_grad = True # 需要计算梯度
def forward(x):
return x * w # w是一个Tensor,所以forward返回的也是一个tensor
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
print("predict (before training)", 4, forward(4).item())
# .item()用于在只包含一个元素的tensor中提取值,输出是一个标量,有多个元素的话使用.tolist()。 w.grad.data则是一个Tensor类型
for epoch in range(100):
for x, y in zip(x_data, y_data):
l = loss(x, y) # l是一个张量,tensor主要是在建立计算图 forward, compute the loss
l.backward()
# 反向传播。调用该方法后w.grad由None更新为Tensor类型,且w.grad.data的值用于后续w.data的更新。
# l.backward()会把计算图中所有需要梯度(grad)的地方都会求出来,然后把梯度都存在对应的待求的参数中,最终计算图被释放。
print('\tgrad:', x, y, w.grad.item())
w.data = w.data - 0.01 * w.grad.data # 权重更新时,注意grad也是一个tensor
w.grad.data.zero_() # 更新一轮后,记得把算出的梯度清零,不然会和后面算出来的梯度叠加
print('progress:', epoch, l.item()) # 取出loss使用l.item,不要直接使用l(l是tensor会构建计算图)
print("predict (after training)", 4, forward(4).item())
predict (before training) 4 4.0
grad: 1.0 2.0 -2.0
grad: 2.0 4.0 -7.840000152587891
grad: 3.0 6.0 -16.228801727294922
progress: 0 7.315943717956543
grad: 1.0 2.0 -1.478623867034912
grad: 2.0 4.0 -5.796205520629883
grad: 3.0 6.0 -11.998146057128906
progress: 1 3.9987640380859375
grad: 1.0 2.0 -1.0931644439697266
grad: 2.0 4.0 -4.285204887390137
grad: 3.0 6.0 -8.870372772216797
………
progress: 98 9.094947017729282e-13
grad: 1.0 2.0 -7.152557373046875e-07
grad: 2.0 4.0 -2.86102294921875e-06
grad: 3.0 6.0 -5.7220458984375e-06
progress: 99 9.094947017729282e-13
predict (after training) 4 7.999998569488525
以及这一节还有两个手动推导反向传播的计算图,很有利于理解反向传播的过程,这里借用一下其他大佬的图。

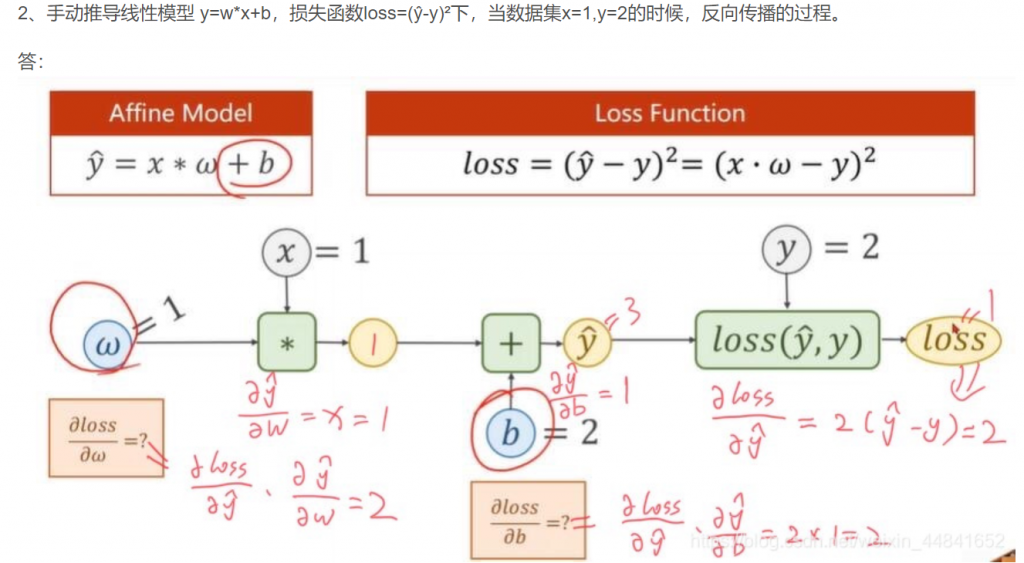
以及y=w1x²+w2x+b的训练过程。
import numpy as np
import matplotlib.pyplot as plt
import torch
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w1 = torch.Tensor([1.0])#初始权值
w1.requires_grad = True#计算梯度,默认是不计算的
w2 = torch.Tensor([1.0])
w2.requires_grad = True
b = torch.Tensor([1.0])
b.requires_grad = True
def forward(x):
return w1 * x**2 + w2 * x + b
def loss(x,y):#构建计算图
y_pred = forward(x)
return (y_pred-y) **2
print('Predict (befortraining)',4,forward(4).item())
for epoch in range(10000):
l = loss(1, 2)#为了在for循环之前定义l,以便之后的输出,无实际意义
for x,y in zip(x_data,y_data):
l = loss(x, y)
l.backward()
print('\tgrad:',x,y,w1.grad.item(),w2.grad.item(),b.grad.item())
w1.data = w1.data - 0.01*w1.grad.data #注意这里的grad是一个tensor,所以要取他的data
w2.data = w2.data - 0.01 * w2.grad.data
b.data = b.data - 0.01 * b.grad.data
w1.grad.data.zero_() #释放之前计算的梯度
w2.grad.data.zero_()
b.grad.data.zero_()
print('Epoch:',epoch,l.item())
print('Predict(after training)',4,forward(4).item())
用pytorch实现线性模型
从这一小节开始,正式使用pytorch的集成功能。
整个代码流程可以分为四步:
- 加载数据集
- 用pytorch的Class类设计model # 目的是为了前向传播forward,即计算y hat(预测值)
- 构造loss和optimizer (使用了 PyTorch API) 其中,计算loss是为了反向传播,optimizer是为了更新梯度。
- 开始训练
其中,训练过程又可以分为:
- 前向传播,求y hat (输入的预测值)
- 根据y_hat和y_label(y_data)计算loss
- 反向传播 backward (计算梯度)
- 根据梯度,更新参数
import torch
import matplotlib.pyplot as plt
# 训练集
# x,y是矩阵,3行1列 也就是说总共有3个数据,每个数据只有1个特征
x_data = torch.tensor([[1.0], [2.0], [3.0]])
y_data = torch.tensor([[2.0], [4.0], [6.0]])
# design model using class
"""
我们的模型类应该继承自nn.Module,它是所有神经网络模块的基类。
必须实现成员方法__init__()和forward()
nn.linear类包含两个分量张量:weight和bias
nn.Linear实现了魔法方法__call__(),它使类的实例可以
像函数一样被调用。通常会调用forward(),forward函数一般会被重载
"""
class LinearModel(torch.nn.Module):
def __init__(self):
super(LinearModel, self).__init__()
# (1,1)是指输入x和输出y的特征维度,这里数据集中的x和y的特征都是1维的,还有第三个参数表示是否加上bias,默认加上
# 该线性层需要学习的参数是w和b 获取w/b的方式分别是~linear.weight/linear.bias
# 注意这里的w和b是pytorch自己生成的,需要的时候会自己计算梯度,所以不需要requires_grad=True
self.linear = torch.nn.Linear(1, 1)
def forward(self, x): # 重载,覆盖
y_pred = self.linear(x)
return y_pred
model = LinearModel() # 定义实例,接下来算函数值只用model(x)就可以了
criterion = torch.nn.MSELoss(reduction='sum')
# 算loss的,括号里的参数为是否除以n,sum表示不除。
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# 优化器,model.parameters()表示把model内的所有参数都求梯度,lr为学习率。注意w和b的初始值是pytorch自己随机取的,已经取好了不用我们自己设置
# 当然计算loss的方法不止SGD一种,可以去查查还有哪些,都可以试试。并且并不是说用了SGD就是随机梯度下降,这个还是看你自己设置的batch大小
# 训练过程
epoch_list=[] # 想画个图,所以设置epoch和loss的容器存储一下每轮的值,方便画图
loss_list=[]
for epoch in range(100):
y_pred = model(x_data) # 求出y_hat
loss = criterion(y_pred, y_data) # 上一步和这一步是前向传播的过程
print(epoch, loss.item())
epoch_list.append(epoch) # 存储画图所需的epch和loss
loss_list.append(loss.item())
optimizer.zero_grad() # 反向传播会再计算梯度,所以在反向传播之前,记得把梯度清零
loss.backward() # 反向传播,会自动计算梯度
optimizer.step() # update 参数,即更新w和b的值
# 输出训练100轮后w和b的值更新成什么数了
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
# 预测一下输入4的时候,y会输出什么
x_test = torch.tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)
#画图
plt.plot(epoch_list,loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()
输出:
0 100.18675994873047
1 44.64421081542969
…..
98 0.01967117004096508
99 0.019388381391763687
w = 1.9073035717010498
b = 0.21072088181972504
y_pred = tensor([[7.8399]])
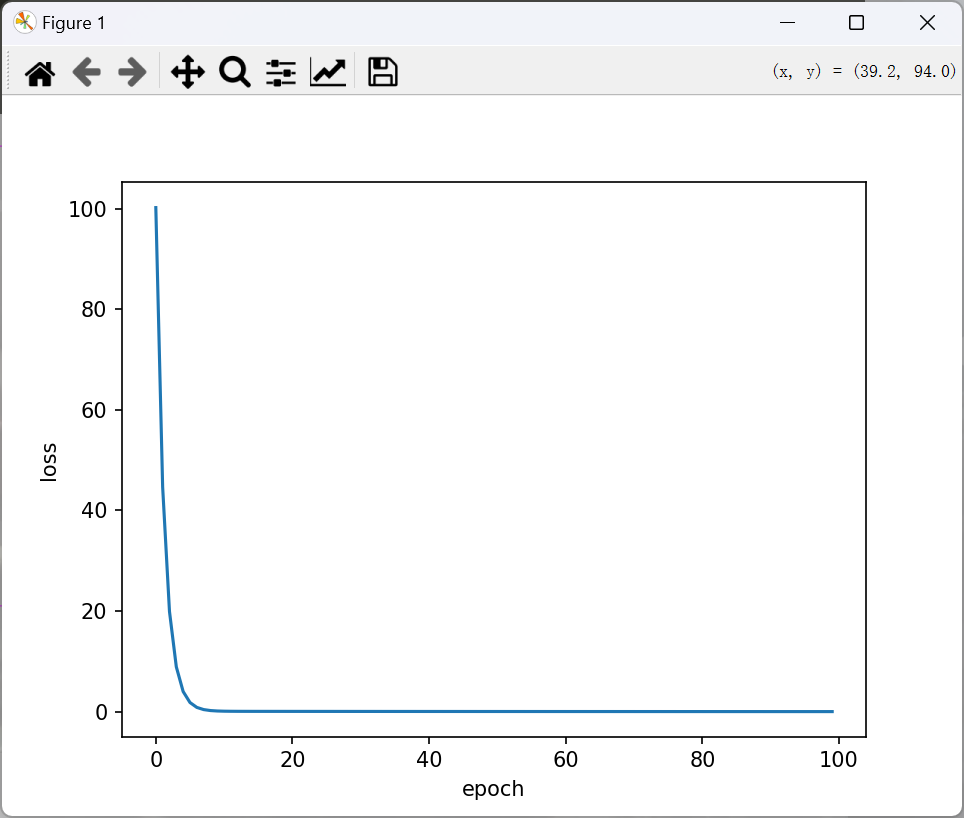
注意:w和b的初始值是pytorch自己取的,因此每运行一次,最后得到的结果都可能是不一样的。其次,轮数和学习率也是可以调节的参数,会影响训练结果。
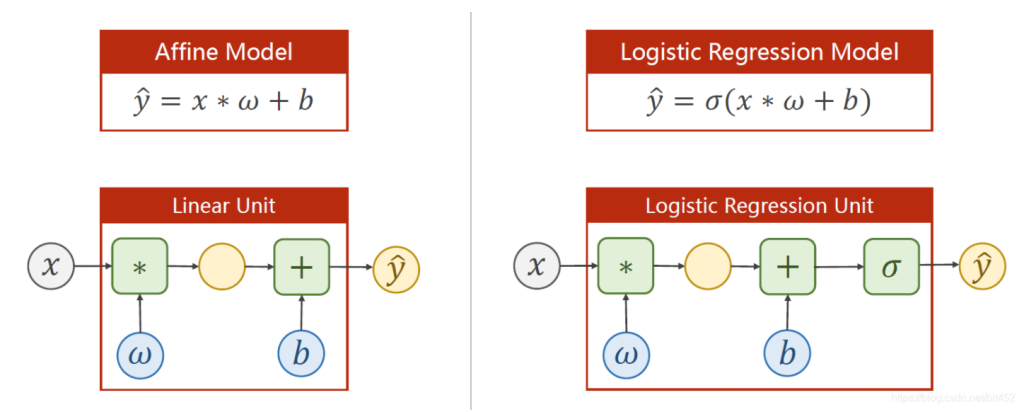
逻辑斯蒂回归模型
说是回归,但逻辑斯蒂解决的其实是分类问题。它与线性模型的不同之处在于它在线性模型之后做了sigmoid变化,将输出值控制在0到1之间,并且输出值代表属于该类的概率。
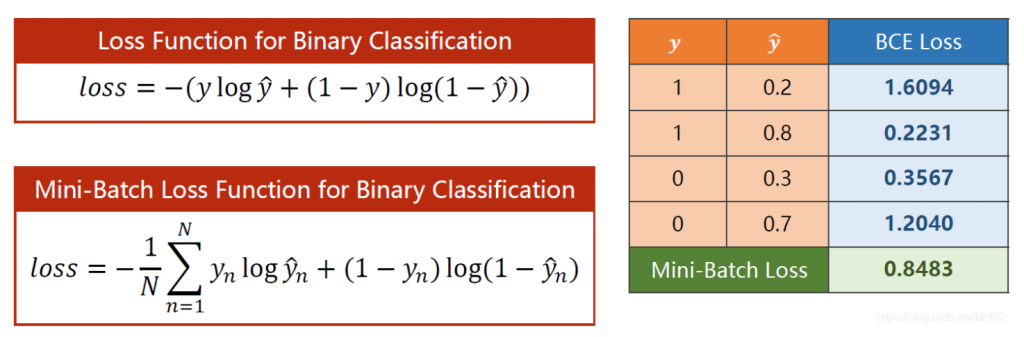
并且计算loss的函数也由MSE变为BCE(交叉熵),也分为除以n和不除以n的版本,交叉熵越大越好,但我们在定义loss函数的时候整体加个负号,变为越小越好,意味着预测与标签越接近。
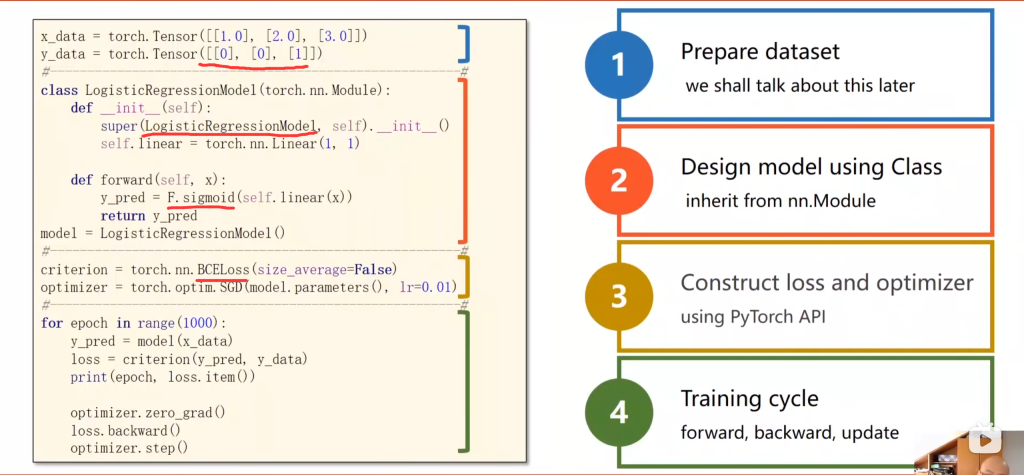
因此,这里用最简单的二分类问题举例,其实还是那四步。和线性模型不同的是:
- 训练集的y_data由一个值变为一个标签。
- 定义model时要将super()内的LinerModel改为LogisticRegressionModel,并且在forward函数里liner后加上sigmoid。
- 在构造损失时将MSEloss改为BCEloss。BCE是交叉熵里用于计算二分类loss的,多分类问题不能用BCE
- 训练过程不变。
import torch
# import torch.nn.functional as F
# prepare dataset
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
# design model using class
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
# y_pred = F.sigmoid(self.linear(x))
y_pred = torch.sigmoid(self.linear(x))
return y_pred
model = LogisticRegressionModel()
# construct loss and optimizer
# 默认情况下,loss会基于element平均,如果size_average=False的话,loss会被累加。
criterion = torch.nn.BCELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# training cycle forward, backward, update
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)
if(y_test.data.item() > 0.5):
print("通过")
else:
print("不能通过")
0 2.209406614303589
1 2.2037758827209473
……..
998 1.0672887563705444
999 1.0667895078659058
w = 1.1629860401153564
b = -2.8110663890838623
y_pred = tensor([[0.8631]])
通过
ps:训练集那里y_data如果报错可以改为Tensor改为tensor,或者把里面的0,0,1改成0.0,0.0,0.1,具体是为什么我也不知道。。。可能是pytorch版本升级了,反正我目前用的没报错。
多维特征的输入
在之前的实验中,数据集的输入x都是一维的,但实际上输出可能和很多因素相关,例如下图就是预测一年后是否会得糖尿病的数据,其中前八列代表不同因素。
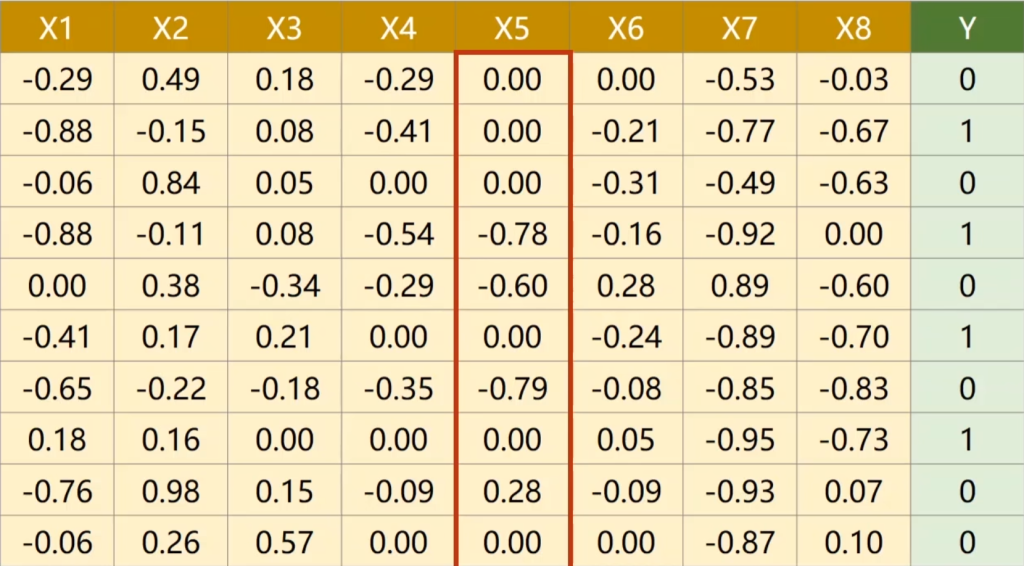
对于计算机来说,多维的输入对应着矩阵的运算,且不同的x特征有不同的权重w。

代码中构造了三层神经网络,第一层是8维到6维的非线性空间变换,第二层是6维到4维的非线性空间变换,第三层是4维到1维的非线性空间变换。
import numpy as np
import torch
import matplotlib.pyplot as plt
# prepare dataset
xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)
# delimiter表示分隔符用的是什么(一般是空格或者逗号)。dtype要用float,因为N卡显卡只支持float32位不支持double64位
x_data = torch.from_numpy(xy[:, :-1]) # 第一个‘:’是指读取所有行,第二个‘:’是指从第一列开始,最后一列不要
y_data = torch.from_numpy(xy[:, [-1]]) # [-1] 最后得到的是个矩阵,不加中括号就变成向量了
# design model using class
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
# 当然神经网络的层数可以自己设置,越深模型的表达能力就越强,但过拟合的风险也会越大
self.linear1 = torch.nn.Linear(8, 6) # 输入数据x的特征是8维,x有8个特征
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
# torch.nn.Sigmoid和上一讲torch.sigmoid()不同,后者是函数,前者是类,前者一般用于激活网络的一层,而不是简单的函数使用
def forward(self, x):
# 按理说每一层的输入都是不一样的,应该用x1,x2...但项目中如果这里参数过多,报错了很难发现是这里的问题,所以约定俗成的在这里用同一个变量x
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x)) # y hat
return x
model = Model()
# 构造 loss and optimizer
# criterion = torch.nn.BCELoss(size_average = True)废弃了
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
epoch_list = [] # 用来画图
loss_list = []
# 训练过程,是一样的
for epoch in range(100):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
# print(epoch, loss.item())
epoch_list.append(epoch)
loss_list.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
plt.plot(epoch_list, loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()
看看loss图像
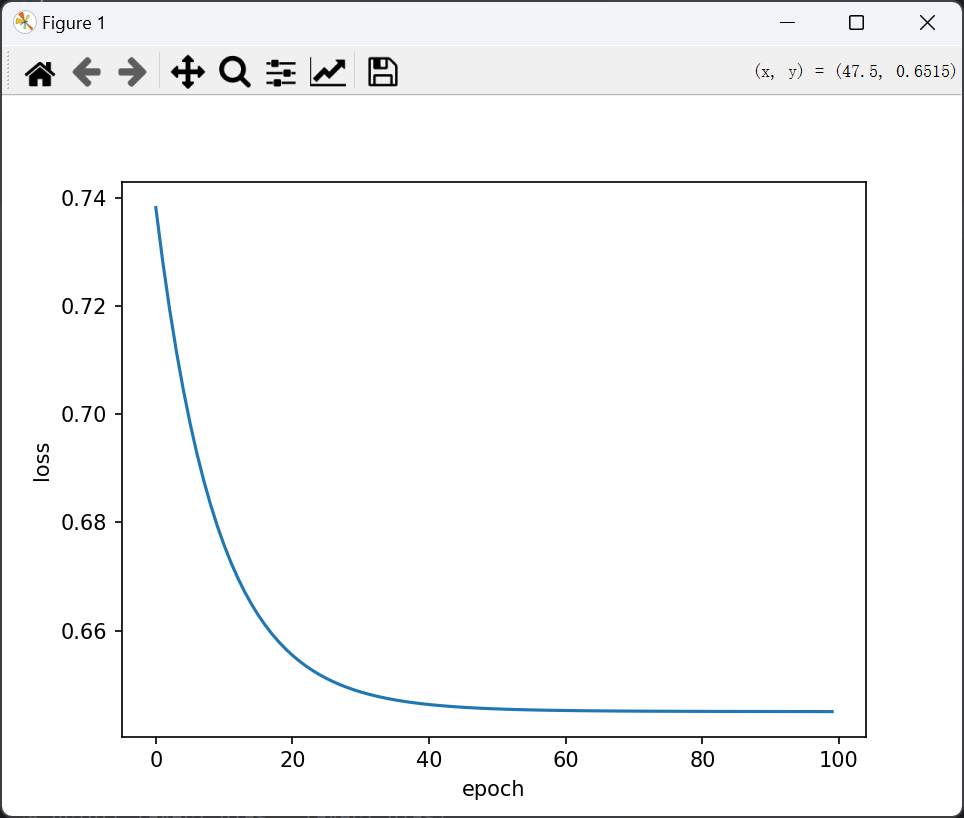
如果想查看某一层的w和b,以第一层为例:
layer1_weight = model.linear1.weight.data
layer1_bias = model.linear1.bias.data
print("layer1_weight", layer1_weight)
print("layer1_weight.shape", layer1_weight.shape)
print("layer1_bias", layer1_bias)
print("layer1_bias.shape", layer1_bias.shape)
layer1_weight tensor([[ 0.1416, 0.1084, -0.1115, -0.2643, 0.2888, -0.0732, -0.0608, 0.3349],
[-0.1333, -0.1775, 0.0798, 0.3215, -0.2651, 0.0455, -0.0261, 0.1355],
[ 0.1601, 0.2246, -0.2489, -0.2026, -0.2431, 0.0449, 0.1280, 0.0297],
[ 0.0985, -0.2630, 0.1223, 0.0633, -0.2472, -0.1116, -0.1593, 0.2212],
[ 0.0112, -0.0110, 0.2589, -0.1451, 0.2921, -0.1886, 0.3219, -0.0928],
[-0.1222, -0.1128, -0.0539, 0.2699, -0.2260, 0.2323, 0.3387, -0.0306]])
layer1_weight.shape torch.Size([6, 8])
layer1_bias tensor([-0.0717, 0.1935, -0.0087, -0.0059, 0.2816, -0.2854])
layer1_bias.shape torch.Size([6])
我们回到loss图像,可以看到训练结束的时候loss依然很大,这时候就需要改进,直接化身调参侠。
可以修改的地方很多,例如增加神经网络的层数,调整学习率,用ReLU代替sigmoid,增大训练轮数,修改优化器(比如把SGD改为Adam)
import numpy as np
import torch
import matplotlib.pyplot as plt
# prepare dataset
xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:, :-1]) # 第一个‘:’是指读取所有行,第二个‘:’是指从第一列开始,最后一列不要
print("input data.shape", x_data.shape)
y_data = torch.from_numpy(xy[:, [-1]]) # [-1] 最后得到的是个矩阵
# print(x_data.shape)
# design model using class
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 2)
self.linear4 = torch.nn.Linear(2, 1)
self.sigmoid = torch.nn.Sigmoid()
self.activate = torch.nn.ReLU()
def forward(self, x):
x = self.activate(self.linear1(x))
x = self.activate(self.linear2(x))
x = self.activate(self.linear3(x))
x = self.sigmoid(self.linear4(x)) # y hat
return x
model = Model()
# construct loss and optimizer
# criterion = torch.nn.BCELoss(size_average = True)
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.05)
# training cycle forward, backward, update
for epoch in range(50000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
# print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 10000 == 9999: # 在1000000次循环中,每100000次打印一次loss和acc
y_pred_label = torch.where(y_pred >= 0.5, torch.tensor([1.0]), torch.tensor([0.0]))
acc = torch.eq(y_pred_label, y_data).sum().item() / y_data.size(0)
print("loss = ", loss.item(), "acc = ", acc)
input data.shape torch.Size([759, 8])
loss = 0.4055244028568268 acc = 0.8221343873517787
loss = 0.38160738348960876 acc = 0.836627140974967
loss = 0.37947073578834534 acc = 0.836627140974967
……
loss = 0.35615280270576477 acc = 0.8537549407114624
loss = 0.32792720198631287 acc = 0.8735177865612648
可以看到最后loss已经降到0.3了,准确率也达到0.87,还可以继续调参的,这里就不折腾了。
加载数据集Dataset和Dataloder
首先介绍三个概念:Epoch:迭代轮数。 Batch size:一次输入的数据量大小。 lteration:有多少个batch

之前的实验中都没有分batch,所以在训练的过程中只有一轮循环,在分了batch后训练过程有两个循环,外层表示迭代一轮,内层表示更新了一个batch。。
Dataset类里有通过下标找到对应数据的getitem(),还有一个返回数据总量的len()。如果是小数据例如上一节的糖尿病表格,可以直接把所有数据读到内存中。如果是大数据,可以通过getitem()在需要的时候调出某一行/列的数据。

加载时候的四个参数分别代表:定义,batch size的大小,分了batch后是否打乱,并行运行的数量是多少。

代码部分说明:
1、mini batch 需要import DataSet和DataLoader
2、继承DataSet的类需要重写init,getitem,len魔法函数。分别是为了加载数据集,获取数据索引,获取数据总量。
3、DataLoader对数据集先打乱(shuffle),然后划分成mini_batch。
4、len函数的返回值 除以 batch_size 的结果就是每一轮epoch中需要迭代的次数。
5、inputs, labels = data中的inputs的shape是[32,8],labels 的shape是[32,1]。也就是说mini_batch在这个地方体现的
import torch
import numpy as np
from matplotlib import pyplot as plt
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
# 第一步:加载数据集
class DiabetesDataset(Dataset): # 重写init,getitem,len魔术方法
def __init__(self, filepath):
xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
self.len = xy.shape[0] # 这一行的意思是,例如糖尿病数据是N行9列,每一行代表一组数据,所以数据集的shape是(N,9),shape【0】就是第一个数据也就是N
self.x_data = torch.from_numpy(xy[:, :-1])
self.y_data = torch.from_numpy(xy[:, [-1]])
def __getitem__(self, index):
return self.x_data[index], self.y_data[index]
def __len__(self):
return self.len
dataset = DiabetesDataset('diabetes.csv.gz')
train_loader = DataLoader(dataset=dataset, batch_size=64, shuffle=True, num_workers=0) # num_workers 多线程
# 第二步:定义函数
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
# 第三步:构造loss和优化器
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
# 第四步:训练。前向传播,反向传播,更新
t = 0 # 以下三个为画图做准备
epoch_list = []
loss_list = []
if __name__ == '__main__': # 若num_worker不是0,则在window系统下需要加这句
for epoch in range(1000):
for i, data in enumerate(train_loader, 0): # enumerate是获取当前是第几次迭代(也就是i),train_loader里有对应的x和y,赋给了data,0表示下标从0开始
epoch_list.append(t)
t += 1
inputs, labels = data # inputs和labels就是x和y
y_pred = model(inputs)
loss = criterion(y_pred, labels)
loss_list.append(loss.item())
print(epoch, i, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.grid(visible=True) # 把网格线画出来
plt.show()
0 0 0.8358690738677979
0 1 0.8264684081077576
0 2 0.8330232501029968
0 3 0.7747925519943237
0 4 0.7312755584716797
0 5 0.785050630569458
0 6 0.7475590109825134
0 7 0.7298625707626343
0 8 0.734067976474762
0 9 0.7445549368858337
0 10 0.7033848166465759
0 11 0.7143331170082092
….
999 0 0.36679425835609436
999 1 0.43548864126205444
999 2 0.3688619136810303
999 3 0.5312755107879639
999 4 0.36935320496559143
999 5 0.6126932501792908
999 6 0.530788242816925
999 7 0.4618630111217499
999 8 0.41108471155166626
999 9 0.4282708168029785
999 10 0.5458270311355591
999 11 0.49995872378349304
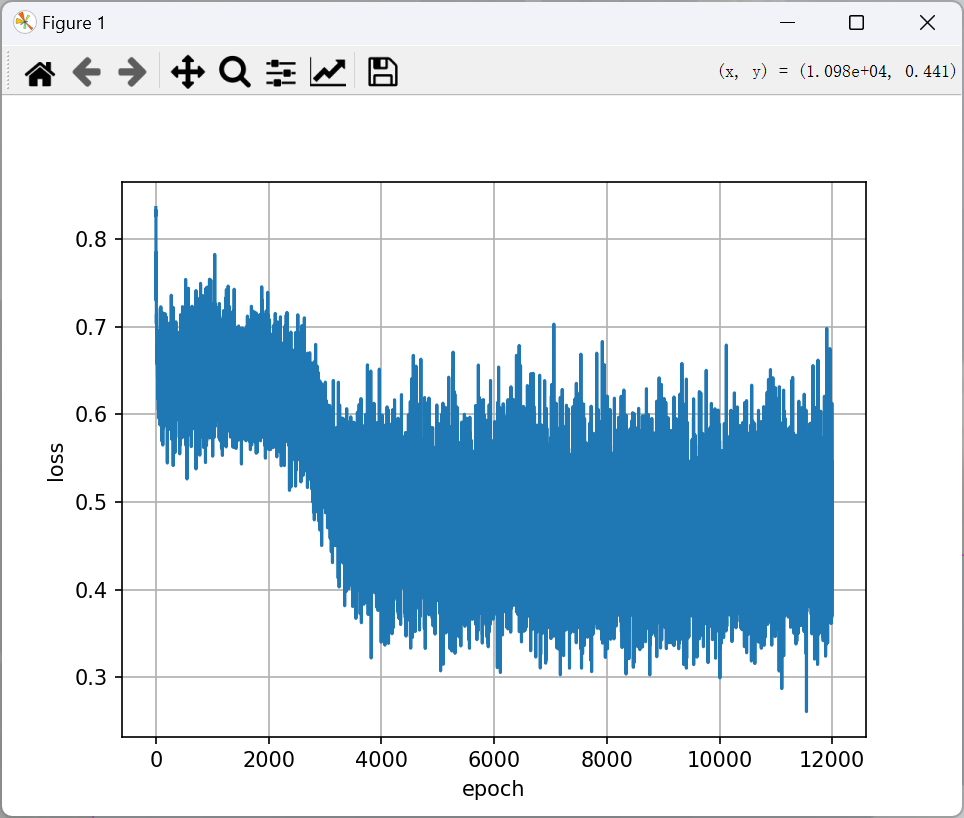
(好抽象的loss……)
多分类问题
1、softmax的输入不需要再做非线性变换,也就是说softmax之前不再需要激活函数(relu)。softmax专门用于多分类问题,sigmoid适用于二分类问题,softmax可以将输出控制在0-1之间,并且让所有输出的总和为1。
2、y的标签编码方式是one-hot。即只有对应标签的那一位是1,其他位都为0。
3、多分类问题,标签y的类型是LongTensor。比如说0-9分类问题,如果y = torch.LongTensor([3]),对应的one-hot是[0,0,0,1,0,0,0,0,0,0].(即下标为3的标签,这里要注意,如果使用了one-hot,标签y的类型是LongTensor,糖尿病数据集中的target的类型是FloatTensor)
4、CrossEntropyLoss <==> LogSoftmax + NLLLoss。也就是说使用CrossEntropyLoss最后一层(线性层)是不需要做其他变化的;使用NLLLoss之前,需要对最后一层(线性层)先进行SoftMax处理,再进行log操作。
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# 第一步:加载训练集
batch_size = 64 # 提前定义batch size大小,方便统一调整大小
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,均值和方差
# 0.137和0.308是提前算好的MNIST数据集的平均值和标准差
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# 第二步:定义函数
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.l1 = torch.nn.Linear(784, 512)
self.l2 = torch.nn.Linear(512, 256)
self.l3 = torch.nn.Linear(256, 128)
self.l4 = torch.nn.Linear(128, 64)
self.l5 = torch.nn.Linear(64, 10)
def forward(self, x):
# 读入的一张图片是N个1×28×28大小的张量,1表示通道(1是黑白,3是rgb三原色也就是彩色),28表示高和宽的像素点个数
x = x.view(-1, 784) # -1其实就是自动获取mini_batch,这一步是把三维的张量转换成一维的向量,以作为神经网络的输入
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
return self.l5(x) # 最后一层不做relu和softmax激活,不进行非线性变换,直接接入下面的交叉熵
model = Net()
# 第三步:构造loss和optimizer
criterion = torch.nn.CrossEntropyLoss() # 这就是交叉熵,包含了softmax+NLLLoss,因此上面的输出层不需要softmax
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5) # momentum就是给梯度下降加上惯性
# 第四步:训练
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
# 获得一个批次的数据和标签,也就是x和y
inputs, target = data
optimizer.zero_grad()
# 获得模型预测结果(64, 10)
outputs = model(inputs)
# 交叉熵代价函数outputs(64,10),target(64)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item() # 每300次updata输出一次平均loss
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def mytest():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader: # 加载测试集
images, labels = data
outputs = model(images) # 输出的每一行代表一个图片的分类结果,最大数(代表最大概率)的下标就是分类的标签
_, predicted = torch.max(outputs.data, dim=1) # dim = 1 列是第0个维度,行是第1个维度,返回值为最大的数及其下标,下划线就是接收一下最大数,但用不到
total += labels.size(0) # labels.size(0)就是N
correct += (predicted == labels).sum().item() # 张量之间的比较运算,看预测和实际标签对上的有几个
print('accuracy on test set: %d %% ' % (100 * correct / total)) # 乘100是因为输出的是百分数
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
mytest()
[1, 300] loss: 2.267
[1, 600] loss: 1.317
[1, 900] loss: 0.461
accuracy on test set: 89 %
[2, 300] loss: 0.338
[2, 600] loss: 0.266
[2, 900] loss: 0.235
……
[9, 300] loss: 0.037
[9, 600] loss: 0.040
[9, 900] loss: 0.042
accuracy on test set: 97 %
[10, 300] loss: 0.030
[10, 600] loss: 0.032
[10, 900] loss: 0.034
accuracy on test set: 97 %
图像作为输入-卷积神经网络CNN
如果忘了CNN的理论,点这里去复习一下
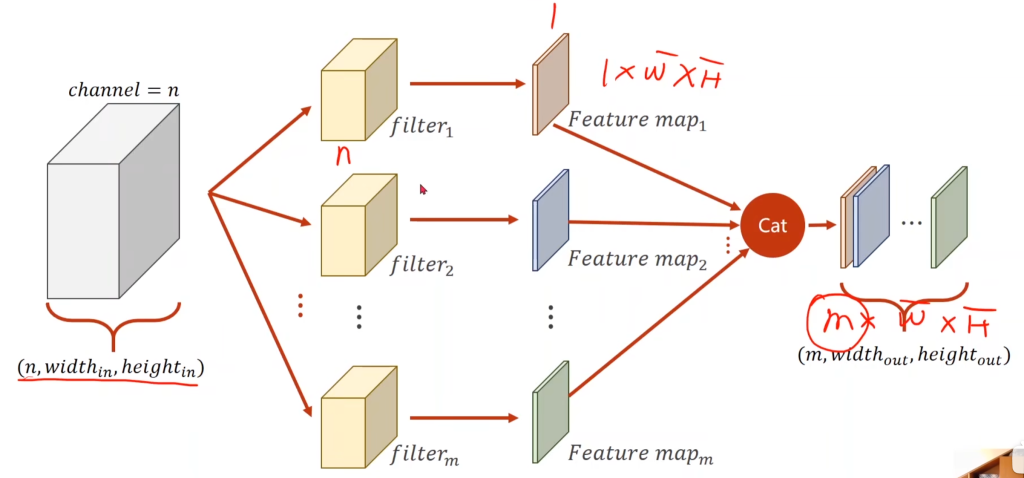
例如一个5×5×3的图像矩阵,分别和3个3×3的矩阵做点乘运算,再把三个结果相加,这个过程就叫做卷积。这个3×3×3的矩阵叫做一个卷积核。由此可以看出:卷积核的通道数量 = 输入图片的通道数量。
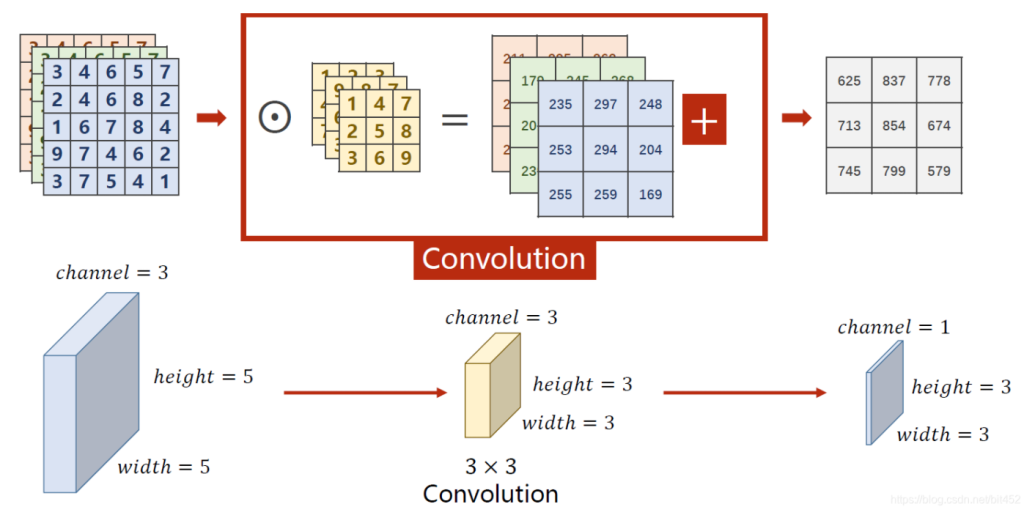
而在理论片也讲过,同一个接受域可以有多个神经元看着,因此可以有多个不同的卷积核与该接受域进行点乘,最后的结果再拼接起来,形成一个m×w×h的矩阵。由此可以看出:卷积核的个数 = 输出通道数
而理论篇里讲的共享参数,指的就是使用同一个卷积核。
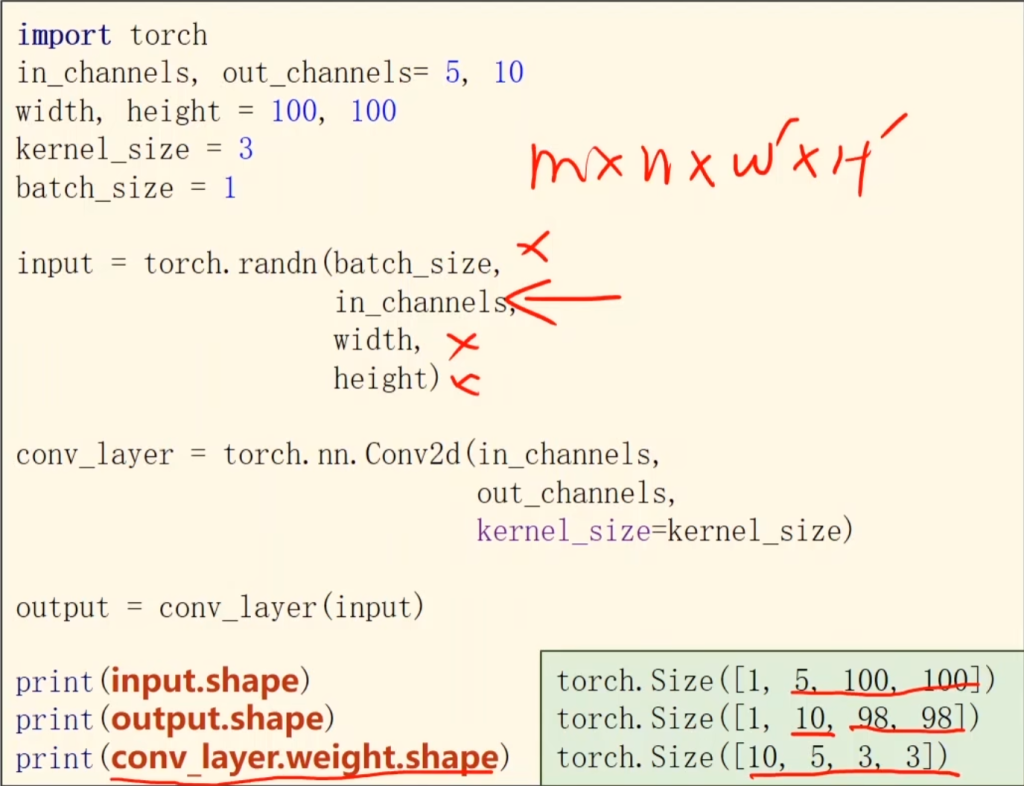
来看一下代码,in_channels和out_channels表示输入通道数和输出通道数。width和height表示输入图片的宽和高,kernel_size表示这是一个3×3的卷积核,卷积核的通道数量和输入通道数一样。
然后再看一下torch.Size输出的结果。第一个输入shape的四个值表示,输入图片的数量,输入通道数,输入图片的宽和高。第二个同理,98因为是3×3的卷积核,起点的圆心在从第三个开始。第三个表示卷积核的数量、卷积核的通道数,卷积核的宽和高。
从这些数值中也可以再次看出上面的结论:输入通道数 = 卷积核的通道数,卷积核的个数 = 输出通道数
接下来讲讲一些CNN里的参数。
① padding(补值):在理论篇里也提到过,如果卷积核在移动到边缘越界了,可以用padding将越界的部分补齐,目的是不会忽视边缘的特征。从输入图片的总体来看,在卷积核为3×3的情况下,padding让输入图片向外扩充了1圈(3/2=1),5×5的卷积核则要扩充两圈(5/2=2)。因此可以看出,卷积层的size最好设置为奇数,根据前人的经验,卷积核size设为3×3,stride设为2是效果最好的。
如下图,input用view转换后的四个参数代表batch、通道数量、输入图片的宽、高。
Conv2d的参数表示:输入通道数、输出通道数,卷积核size,向外扩充几圈,是否加上偏差值b。
kernel的view转换参数表示:输入通道数,输出通道数,卷积核的宽,卷积核的高

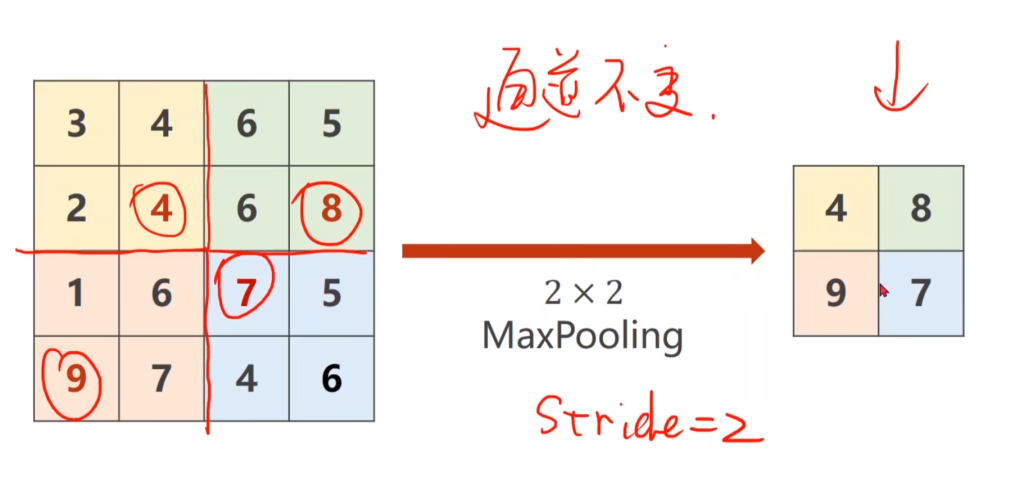
② 最大池化:例如当卷积核为2×2时,默认的stride也 为2,那么最大池化就是把原图按2×2为一个单位割开,然后找每个单位里最大的数(这里我的理解是提取有效特征),由于池化层只是做切割,因此输入图片的通道数不变。实现的代码也如右下。

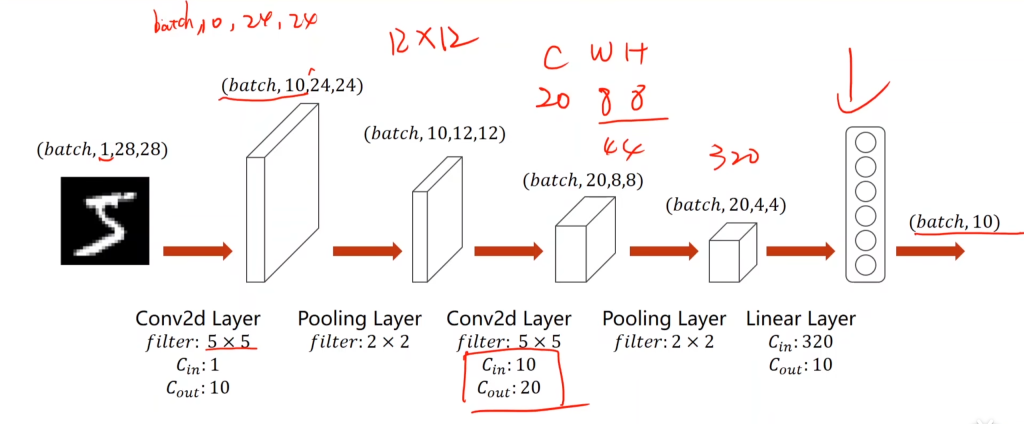
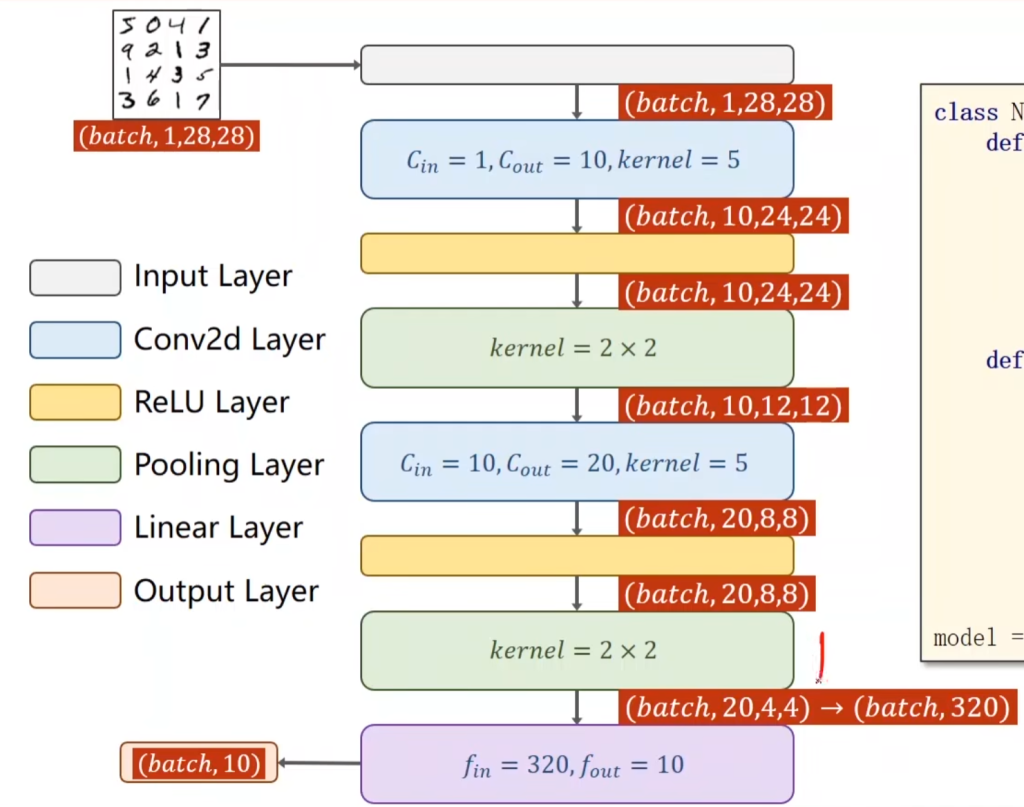
最后来看CNN的总流程:
通道数为1的28×28的图片,经过第一个卷积层,该卷积层的卷积核为5×5,数量为10,因此输出通道数为10,输出大小为24×24(因为没有padding,减掉了4)
接着经过第一个池化层,该池化层的卷积核为2×2,因此宽和高减半,且输出通道数不变,为10。
接着经过第二个卷积层,该卷积层的卷积核为5×5,输入通道数为10,卷积核个数为20,因此输出通道数为20,因为没有padding,宽和高继续减4.输出大小为8×8.
接着经过第二个池化层,该池化层的卷积核为2×2,因此宽和高减半,且输出通道数不变,为20.
接着,将该20×4×4(=320)矩阵转换为一维向量,然后接入一个全连接层,将320维转化为10维(因为最后分类有十类)。
最后,用softmax将其变为多分类问题的输出。
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# 第一步:加载数据集
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
# 0.137和0.308是提前算好的MNIST数据集的均值和方差
# 这段代码是使用PyTorch中的transforms.Compose函数创建了一个转换操作的序列。其中包括了两个转换操作:ToTensor和Normalize。
# ToTensor将图像转换为PyTorch张量,而Normalize则对张量进行标准化处理,通过减去均值并除以方差来对数据进行归一化。
# 这种预处理常用于准备图像数据以输入神经网络模型,可以消除偏差,提高模型性能,减少噪声影响
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# 第二步:定义Model
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5) # 输入通道为1,卷积核数量为10,输出通道为10的第一个卷积层
self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5) # 输入通道为10,卷积核数量为20,输出通道为20的第二个卷积层
self.pooling = torch.nn.MaxPool2d(2) # 最大池化层,卷积核为2×2,stride也为2
self.fc = torch.nn.Linear(320, 10) # 这个320是上面那幅图里提前算出来的
def forward(self, x):
# flatten data from (n,1,28,28) to (n, 784)
batch_size = x.size(0)
x = self.pooling(F.relu(self.conv1(x)))
x = self.pooling(F.relu(self.conv2(x)))
x = x.view(batch_size, -1) # -1 此处自动算出的是320,其实我感觉-1就是让计算机自己算出这个位置的参数值是多少的意思,多分类问题是第一个参数-1
x = self.fc(x) # 再次强调最后要接入交叉熵的,所以最后一层不做激活!
return x
model = Net()
# 下面的代码和上一节一模一样
# 第三步:构造loss和optimizer
criterion = torch.nn.CrossEntropyLoss() # 交叉熵 = softmax + NLLLoss
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# 第四步:训练
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def mytest():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('accuracy on test set: %d %% ' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
mytest()
[1, 300] loss: 0.563
[1, 600] loss: 0.186
[1, 900] loss: 0.140
accuracy on test set: 95 %
[2, 300] loss: 0.110
[2, 600] loss: 0.097
[2, 900] loss: 0.089
accuracy on test set: 97 %
……
[10, 300] loss: 0.032
[10, 600] loss: 0.040
[10, 900] loss: 0.038
accuracy on test set: 98 %
以下为使用GPU训练的代码,其实也就加了四行代码而已:
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# 第一步:加载数据集
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
# 0.137和0.308是提前算好的MNIST数据集的均值和方差
# 这段代码是使用PyTorch中的transforms.Compose函数创建了一个转换操作的序列。其中包括了两个转换操作:ToTensor和Normalize。
# ToTensor将图像转换为PyTorch张量,而Normalize则对张量进行标准化处理,通过减去均值并除以方差来对数据进行归一化。
# 这种预处理常用于准备图像数据以输入神经网络模型,可以消除偏差,提高模型性能,减少噪声影响
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# 第二步:定义Model
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5) # 输入通道为1,卷积核数量为10,输出通道为10的第一个卷积层
self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5) # 输入通道为10,卷积核数量为20,输出通道为20的第二个卷积层
self.pooling = torch.nn.MaxPool2d(2) # 最大池化层,卷积核为2×2,stride也为2
self.fc = torch.nn.Linear(320, 10) # 这个320是上面那幅图里提前算出来的
def forward(self, x):
# flatten data from (n,1,28,28) to (n, 784)
batch_size = x.size(0)
x = self.pooling(F.relu(self.conv1(x)))
x = self.pooling(F.relu(self.conv2(x)))
x = x.view(batch_size, -1) # -1 此处自动算出的是320,其实我感觉-1就是让计算机自己算出这个位置的参数值是多少的意思,多分类问题是第一个参数-1
x = self.fc(x) # 再次强调最后要接入交叉熵的,所以最后一层不做激活!
return x
model = Net()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") #这一行和下面一行是调用显卡来训练
model.to(device)
# 下面的代码和上一节一模一样
# 第三步:构造loss和optimizer
criterion = torch.nn.CrossEntropyLoss() # 交叉熵 = softmax + NLLLoss
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# 第四步:训练
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
inputs, target = inputs.to(device), target.to(device) # 这一行也是用了显卡训练之后要把输入输出数据存到显卡上,所以调用显卡只需要三行代码
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def mytest():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
images, labels = images.to(device), labels.to(device) # 同上显卡存数据,是四行代码
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('accuracy on test set: %d %% ' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
mytest()
CNN进阶篇:网络结构的封装及残差网络
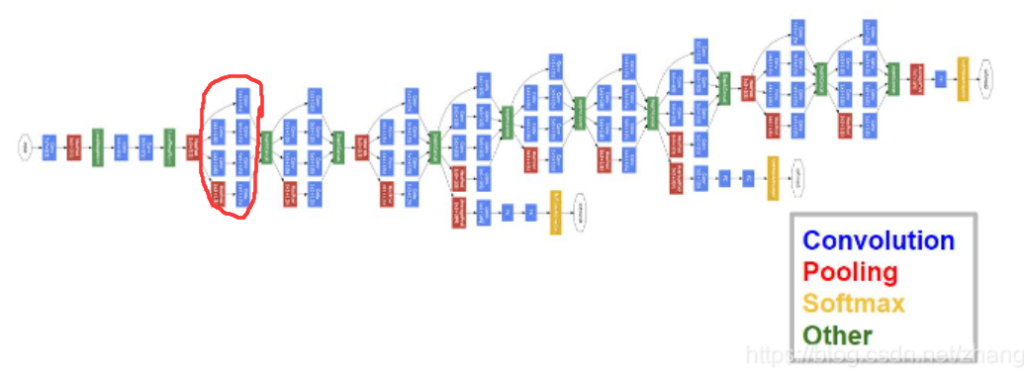
在上面的实验中,模型网络的构造都是只有几层、非常简单的网络,但在项目实操中,网络的结构往往是非常复杂的,例如下图名为GoogleNet的网络就是非常经典的模型,很多模型都是在这个模型基础上改的。
但这种模型非常复杂,一层一层构造很麻烦,但我们发现网络中有很多重复的结构(圈出来的部分),因此我们就可以用封装的思想将这种重复的结构打包起来,然后需要的时候直接调用。
这种“封装”的过程称为Inception Moudel,接下来以封装右图的结构为例,展示Inception Moudel如何构造。(Inception Moudel可以自己设计结构的)
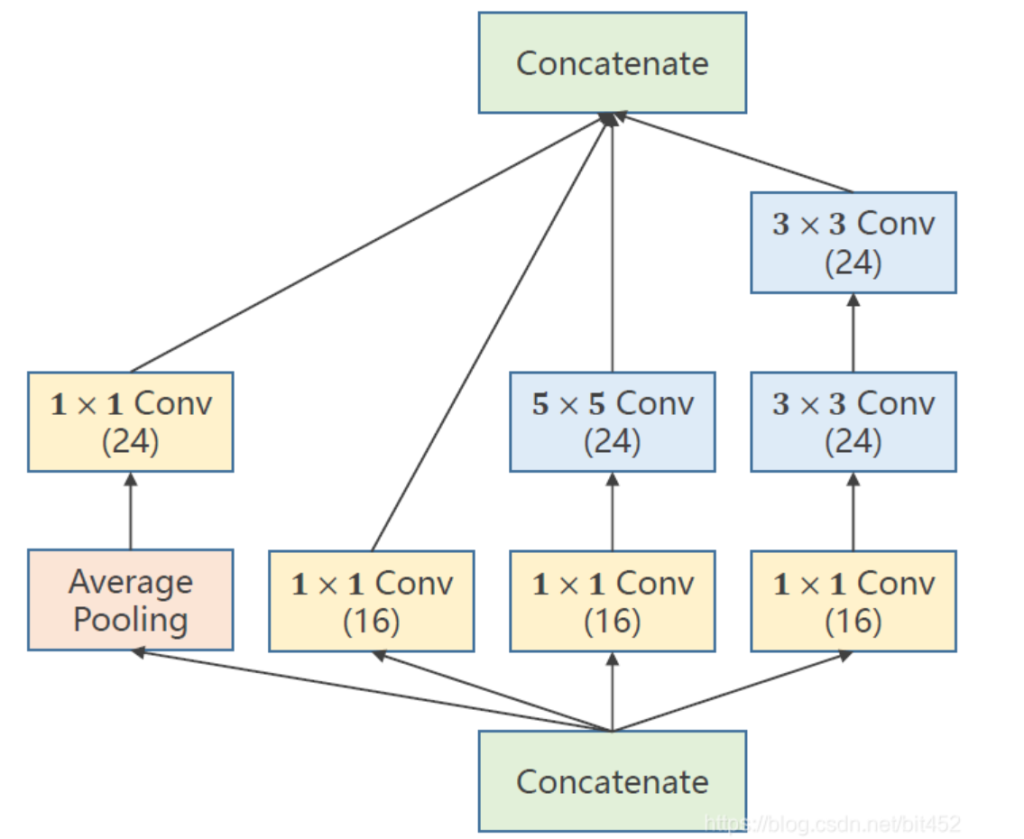
构造过程也很容易理解,(branch是分支的意思)
其中平均池化层设置卷积核size3×3,padding=1是为了不改变原图的宽高。下面的也是不改变原图的宽高,方便最后拼接起来。
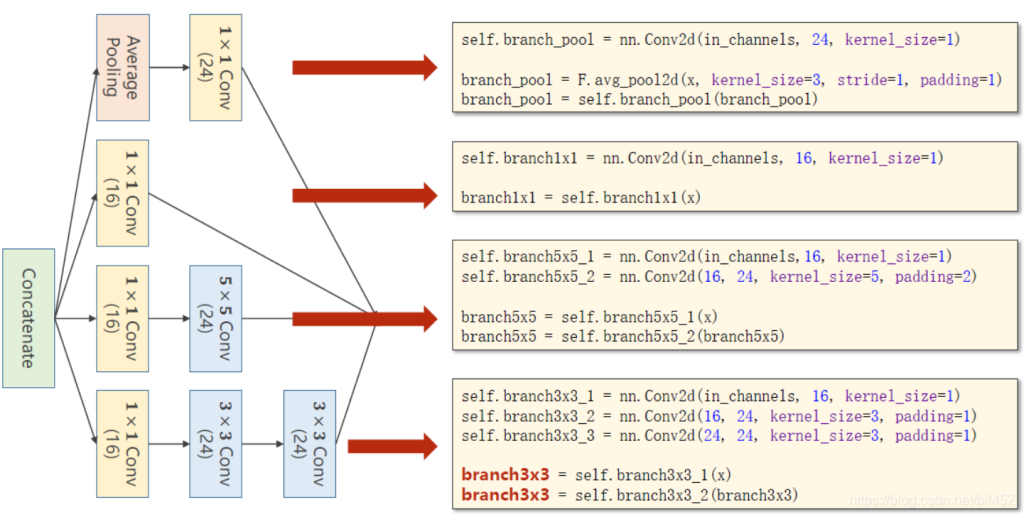
以下是代码部分:
- 先用类对Inception Moudel封装
- 模型的结构为:先是1个卷积层(conv,maxpooling,relu,(1,10)),然后inceptionA模块(输出的channels是24+16+24+24=88(10,88)),接下来又是一个卷积层(conv,mp,relu,(88,20)),然后inceptionA(20,88)模块,然后用view拉成一维向量(1*28*28 → 10*24*24 → 10*12*12 → 88*12*12 → 20*8*8 → 88*4*4=1408)最后一个全连接层(fc)。
- 1408这个数据可以通过x = x.view(in_size, -1)后调用x.shape得到。
import torch
import torch.nn as nn
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# 第一步:加载数据集
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# 第二步:定义模型函数
# 封装Inception Moudle
class InceptionA(nn.Module):
def __init__(self, in_channels):
super(InceptionA, self).__init__()
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)
self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)
def forward(self, x):
branch1x1 = self.branch1x1(x)
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
branch3x3 = self.branch3x3_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
branch_pool = self.branch_pool(branch_pool)
outputs = [branch1x1, branch5x5, branch3x3, branch_pool] # 这一步是把四个分支拼接到一块,之所以能拼接是因为四个分支输出的宽高都一样,只是通道数变了
return torch.cat(outputs, dim=1) # b,c,w,h c对应的是dim=1,意思是按照通道数的方向拼接,最后拼出来的总通道数为c=16+24+24+24=88,
# 也就是每经过一次Inception通道数都会变为88
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5) # 手写数字图片是黑白的,输入通道为1
self.conv2 = nn.Conv2d(88, 20, kernel_size=5) # 88上面算过了
self.incep1 = InceptionA(in_channels=10) # 与conv1 中的10对应
self.incep2 = InceptionA(in_channels=20) # 与conv2 中的20对应
self.mp = nn.MaxPool2d(2)
self.fc = nn.Linear(1408, 10)
# 1*28*28 → 10*24*24 → 10*12*12 → 88*12*12 → 20*8*8 → 88*4*4=1408
def forward(self, x):
in_size = x.size(0)
x = F.relu(self.mp(self.conv1(x)))
x = self.incep1(x)
x = F.relu(self.mp(self.conv2(x)))
x = self.incep2(x)
x = x.view(in_size, -1)
x = self.fc(x) # 第n次强调,后面接交叉熵,所以不需要激活
return x
model = Net()
# 第三步:构造loss和optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# 第四步:训练
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def mytest():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('accuracy on test set: %d %% ' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
mytest()
循环神经网络RNN
RNN cell的用法
如果忘了RNN的理论,点这里去复习一下
在RNN里,当前的输出不仅和当前的输入有关,还和上一次循环所存储的信息(记为hidden)有关。因此,在RNN内部,需要将xt和ht-1的信息融合(具体是将二者都做线性变化到同维,然后相加),然后再做激活,RNN的激活函数一般不用sigmoid,tanh用的比较多。
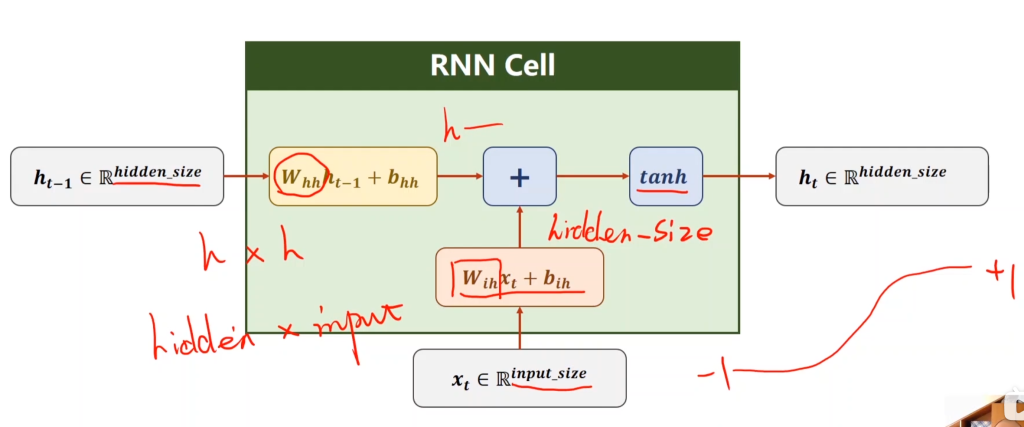
RNN刚开始学着难是因为搞不清楚每个参数的维度,只要搞清楚了参数的维度,pytorch的代码就可以看的懂了。
如果是自己设置RNN cell,那么输入有两个:一个是当前的input,维度是batch×input size,batch = 训练集总数 / batch size,input size取决于输入,例如用温度、气压、时期来预测降雨率,那么输入维度(input size)就是3。另一个是上一次循环保存的hidden,维度是batch×hidden。
输出有一个:维度和hidden相同
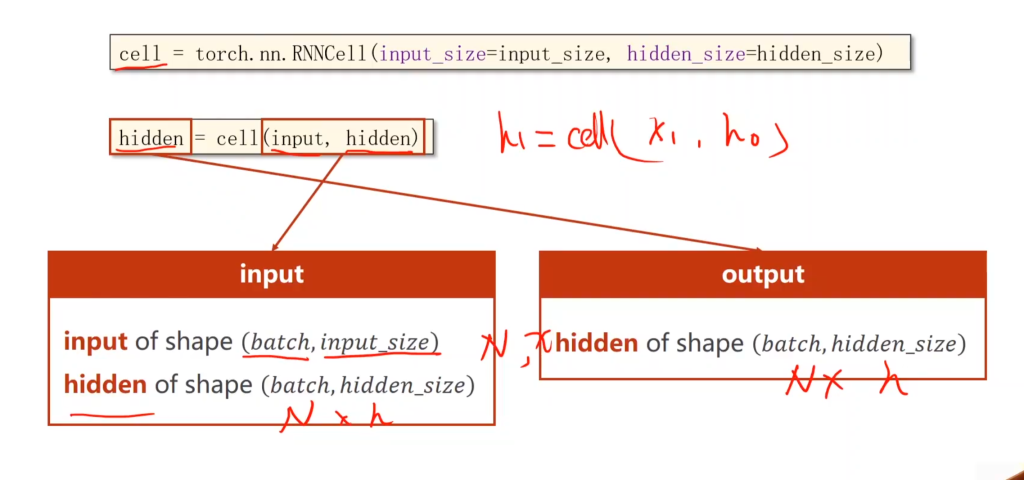
import torch
batch_size = 1 # 批处理大小
seq_len = 3 # 序列长度
input_size = 4 # 输入维度
hidden_size = 2 # 隐藏层维度
cell = torch.nn.RNNCell(input_size=input_size, hidden_size=hidden_size)
# (seq, batch, features)
dataset = torch.randn(seq_len, batch_size, input_size)
print(dataset)
hidden = torch.zeros(batch_size, hidden_size)
print(hidden)
for idx, input in enumerate(dataset):
print( '=' * 20, idx, '=' * 20)
print( 'Input size: ', input.shape)
hidden = cell(input, hidden)
print( 'outputs size: ', hidden.shape)
print(hidden)
RNN的用法
如果还是不清晰,拿自然语言处理为例: batchsize 相当于一次性训练几句话, seqlen 相当于一句话有几个字, inputsize 就是一个字要转为向量才能输入,这个向量的维度就是input size(词嵌入向量维度)
或者拿之前的预测降雨率举例子:batch每次训练一个样本、seqlen每个样本3天的天气数据、input size每天有4个特征的输入,并使用hidden =2维的隐藏状态来学习和预测天气情况
对于机器来说,就是batch_size一次性扔进去多少个样本训练,seq_len是RNN中循环多少次,input_size是输入的特征数,hidden_size是输出的特征数
如果是直接用pytorch自带的RNN,那就更简单了,连循环都不用写。输入是inputs和hidden,输出是out和hidden,对应图中所示
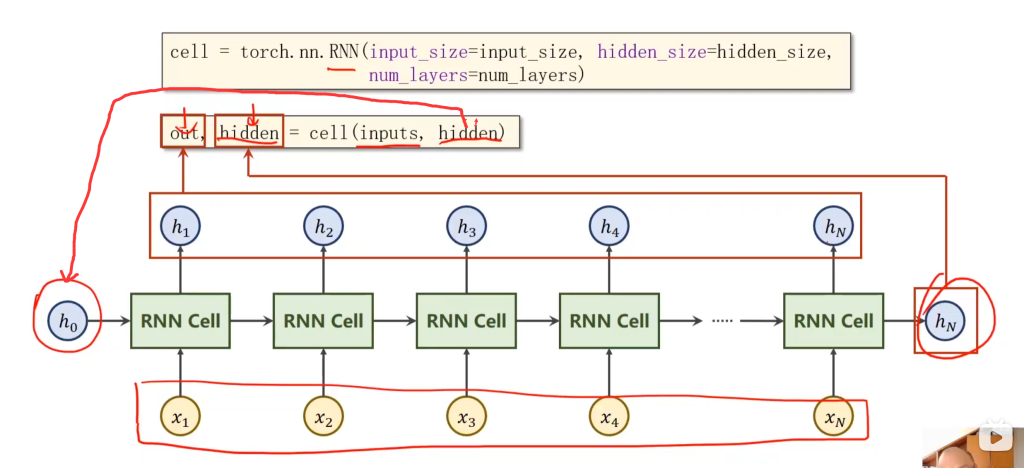
于是,相比于RNN cell,RNN的input、hidden和outputs的维度有所改变:
input和ouput多加了个seqlen参数(用来代替循环),hidden多加了numLayers参数,用来表示RNN有多少层。

import torch
# 1、确定参数
seq_len = 5
input_size = 4
hidden_size = 4
batch_size = 1
num_layers = 1
# 2、准备数据
index2char = ['e', 'h', 'l', 'o'] # 字典
x_data = [1, 0, 2, 2, 3] # 用字典中的索引(数字)表示来表示hello
y_data = [3, 1, 2, 3, 2] # 标签:ohlol
one_hot_lookup = [[1, 0, 0, 0], # 用来将x_data转换为one-hot向量的参照表
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]]
x_one_hot = [one_hot_lookup[x] for x in x_data]
# 遍历 x_data 列表中的每个元素 x。
# 对于每个元素 x,它在 one_hot_lookup 字典中查找对应的独热编码向量。
# 将找到的独热编码向量添加到一个新的列表 x_one_hot 中。
# 最终,x_one_hot 列表将包含与 x_data 中每个原始数据值对应的独热编码向量。
# 独热编码是一种常用的数据预处理技术,它将每个类别或数值转换为一个二进制向量,其中只有一个元素是1(表示该类别或数值),其余都是0。这种方法常用于机器学习中的特征工程,尤其是在处理分类问题时。
inputs = torch.Tensor(x_one_hot).view(seq_len, batch_size,input_size) # (𝒔𝒆𝒒𝑳𝒆𝒏,𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒊𝒏𝒑𝒖𝒕𝑺𝒊𝒛𝒆)
labels = torch.LongTensor(y_data)
# 3、构建模型
class Model(torch.nn.Module):
def __init__(self, input_size, hidden_size, batch_size, num_layers=1):
super(Model, self).__init__()
self.num_layers = num_layers
self.batch_size = batch_size
self.input_size = input_size
self.hidden_size = hidden_size
self.rnn = torch.nn.RNN(input_size=self.input_size, hidden_size=self.hidden_size, num_layers=num_layers)
def forward(self, input):
hidden = torch.zeros(self.num_layers, self.batch_size, self.hidden_size)
# 这一步是构建h0,因为后面的训练都有前一次ht-1,第一次没有,所以要构建一个
out, _ = self.rnn(input, hidden) # out: tensor of shape (seq_len, batch, hidden_size)
return out.view(-1, self.hidden_size) # 将输出的三维张量转换为二维张量,(𝒔𝒆𝒒𝑳𝒆𝒏×𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒉𝒊𝒅𝒅𝒆𝒏𝑺𝒊𝒛𝒆),方便计算交叉熵
def init_hidden(self): # 初始化隐藏层,需要batch_size
return torch.zeros(self.batch_size, self.hidden_size)
net = Model(input_size, hidden_size, batch_size, num_layers)
# 4、损失和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05) # Adam优化器
# 5、训练
for epoch in range(15):
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
_, idx = outputs.max(dim=1) # 在hidden维度找最大值,也就是看输出哪个的概率最大
idx = idx.data.numpy()
print('Predicted string: ', ''.join([index2char[x] for x in idx]), end='')
print(', Epoch [%d/15] loss: %.4f' % (epoch + 1, loss.item()))



Comments NOTHING